"You shouldn’t do art"
I was told this over and over growing up as a kid. "Your mind doesn’t work that way," being the rationale for this. Teachers, if you are reading this, NEVER tell a kid that. Seriously. I believed it for nearly a half-century, then wrote my first novel, and later painted my first-ever oil painting. Anyone can do art of some kind.
To be fair to those teachers of long ago, my mind does like orderly art. I struggle with understanding impressionist art, but realism and abstraction both move me in ways I never thought possible: Realism, because it tells a story, and abstraction, because I strive to understand what is being abstracted, and can spend hours staring at an abstract painting and trying to grok the fulln…
"You shouldn’t do art"
I was told this over and over growing up as a kid. "Your mind doesn’t work that way," being the rationale for this. Teachers, if you are reading this, NEVER tell a kid that. Seriously. I believed it for nearly a half-century, then wrote my first novel, and later painted my first-ever oil painting. Anyone can do art of some kind.
To be fair to those teachers of long ago, my mind does like orderly art. I struggle with understanding impressionist art, but realism and abstraction both move me in ways I never thought possible: Realism, because it tells a story, and abstraction, because I strive to understand what is being abstracted, and can spend hours staring at an abstract painting and trying to grok the fullness of it.
Which brings us to Piet Mondrian. Surely you’ve heard of this famous Dutch man, a pioneer of 20th-century abstract art who believed that to properly abstract reality, we should use as little reality as possible? No? Well, maybe you’ve seen his work:

So looking at Tableau I here, I think to myself, "Self, could you teach a computer to do that?" and I answered, "Self, I betcha we can."
A bit of noodling around on the web discovered that someone had already done this in Python, and I liked their basic approach—use some configurable random number generators to generate a virtual canvas. But let’s extend that some in the Perl instance. I’d like to have it working with close to Mondrian-correct colors as shown in Tableau I, and be able to output JPG, PNG, and SVG instead of the terminal. I’ll use Moo, mostly because I like Moo, and it makes this generator into a modular object you could use later to store/retrieve specifications of Mondrian-styled paintings, if you want. Let’s get started:
# Required:## cpan Moo Svg::Simple Imager Imager::File::PNG Imager::File::JPEGpackage Acme::Mondrian::Generator;use strict;use warnings;use Moo;use Svg::Simple;use Imager;use Imager::File::PNG; # We don't actually have to include these here, but they mustuse Imager::File::JPEG; # be installed!# Stuff the user can control on creation, with defaultshas resolution => ( is => 'ro', default => sub { return 80 } ); # width in cellshas aspect => ( is => 'ro', default => sub { return 0.75 } ); # height = width * aspecthas line_thickness => ( is => 'ro', default => sub { return 4 } ); # SVG black line thicknesshas scale_px => ( is => 'ro', default => sub { return 20 } ); # px per cell in PNG/SVGhas palette => ( is => 'ro', default => sub { # I did some googling around for these, then asked ChatGPT for the # RGB numbers. return { # I used I<Tableau I> and an eyedropper tool for the web for these. white => [ 224, 220, 221 ], # lead white approximation black => [ 54, 37, 36 ], # bone + carbon black red => [ 246, 68, 58 ], # hematite / iron-oxide red yellow => [ 238, 184, 42 ], # mix: cadmium yellow / ochre / chrome yellow blue => [ 48, 50, 124 ], # dark blue } });# Logical canvas (grid)has canvas => ( is => 'rw', default => sub { return {} } );has width => ( is => 'rw' ); # We'll calculate these at runtime.has height => ( is => 'rw' );1;
Okay, let’s start working on the generator; this is the fiddly bit of the whole problem. In sub generate, which will need no parameters other than the object it$self, we can start by calculating and initializing the whole "canvas":
sub generate { my $self = shift; my $W = $self->resolution; my $H = int( $self->resolution * $self->aspect ); $self->width($W); $self->height($H); my %canvas; $self->canvas( \%canvas ); # Initialize white grid for my $x ( 0 .. $W - 1 ) { for my $y ( 0 .. $H - 1 ) { $canvas{"$x,$y"} = 'white'; } }
Next, we need some lines, both vertical and horizontal. You could do these in either order, I suppose, but I’ll start with vertical lines, then do horizontals. I’m not usually a fan of lexical blocks like this, but it keeps Perl::Critic and Test::NoWarnings happier, by avoiding redefining $x and $y in a haphazard way.
# Random thick grid lines like Mondrianmy $min_x_gap = int($W/10);my $max_x_gap = int($W/5);my $min_y_gap = int($H/10);my $max_y_gap = int($H/5);my $numberOfSegmentsToDelete = 0;# Vertical linesmy @vlines;{ my $x = int( rand( $max_x_gap - $min_x_gap + 1 ) ) + $min_x_gap; while ( $x < $W - $min_x_gap ) { $numberOfSegmentsToDelete++; push @vlines, $x; for my $y ( 0 .. $H - 1 ) { $canvas{"$x,$y"} = 'black' } $x += int( rand( $max_x_gap - $min_x_gap + 1 ) ) + $min_x_gap; }}# Horizontal linesmy @hlines;{ my $y = int( rand( $max_y_gap - $min_y_gap + 1 ) ) + $min_y_gap; while ( $y < $H - $min_y_gap ) { push @hlines, $y; for my $x ( 0 .. $W - 1 ) { $canvas{"$x,$y"} = 'black' } $y += int( rand( $max_y_gap - $min_y_gap + 1 ) ) + $min_y_gap; }}
If we were to output $canvas, we’d get a random canvas of black lines and white blocks, with the lines unevenly spaced. There should be between five and ten of each, based on the max and min gaps above.
Mondrian did not always have his lines going all the way across; as you can see in Tableau I, he would occasionally delete one. This part is a bit tricky, as we need to find a single segment of line at a time.
my $numberOfRectanglesToPaint = $numberOfSegmentsToDelete - 3;$numberOfSegmentsToDelete = int( $numberOfSegmentsToDelete * 1.5 );# Delete a segmentfor ( 1 .. $numberOfSegmentsToDelete ) { while (1) { # let's look for a black spot on the canvas. my $startx = int( rand( $W - 2 ) ) + 1; my $starty = int( rand( $H - 2 ) ) + 1; next if $canvas{"$startx,$starty"} eq 'white'; my $orientation; # Are we on a vertical line, or a horizontal if ( $canvas{ ( $startx - 1 ) . ",$starty" } eq 'white' && $canvas{ ( $startx + 1 ) . ",$starty" } eq 'white' ) { $orientation = 'vertical'; } elsif ($canvas{ "$startx," . ( $starty - 1 ) } eq 'white' && $canvas{ "$startx," . ( $starty + 1 ) } eq 'white' ) { $orientation = 'horizontal'; } else { # We're at an intersection, so don't delete here. next; } my @points = ("$startx,$starty"); my $canDelete = 1; # now find the collection of points on the rest of that segment, and push # them into @points. if ( $orientation eq 'vertical' ) { for my $dy ( -1, 1 ) { my $yy = $starty; while ( $yy > 0 && $yy < $H - 1 ) { $yy += $dy; my $l = $canvas{ ( $startx - 1 ) . ",$yy" }; my $r = $canvas{ ( $startx + 1 ) . ",$yy" }; if ( $l eq 'black' && $r eq 'black' ) { last; } elsif (( $l eq 'white' && $r eq 'black' ) || ( $l eq 'black' && $r eq 'white' ) ) { $canDelete = 0; last; } push @points, "$startx,$yy"; } last unless $canDelete; } } else { # horizontal for my $dx ( -1, 1 ) { my $xx = $startx; while ( $xx > 0 && $xx < $W - 1 ) { $xx += $dx; my $u = $canvas{ "$xx," . ( $starty - 1 ) }; my $d = $canvas{ "$xx," . ( $starty + 1 ) }; if ( $u eq 'black' && $d eq 'black' ) { last; } elsif (( $u eq 'white' && $d eq 'black' ) || ( $u eq 'black' && $d eq 'white' ) ) { $canDelete = 0; last; } push @points, "$xx,$starty"; } last unless $canDelete; } } next unless $canDelete; $canvas{$_} = 'white' for @points; last; }}
A 1-cell black border around the image would be nice:
# Borderfor my $xx ( 0 .. $W - 1 ) { $canvas{"$xx,0"} = 'black'; $canvas{ "$xx," . ( $H - 1 ) } = 'black';}for my $yy ( 0 .. $H - 1 ) { $canvas{"0,$yy"} = 'black'; $canvas{ ( $W - 1 ) . ",$yy" } = 'black';}
Okay, now the next hard part, painting in a few rectangles. In this case, we’re going to look for white space, then continue filling white space around it recursively until we hit a line.
# Flood fill rectanglesmy @fillcolors = qw(red yellow blue white white white); # biased toward whitemy %seen;for ( 1 .. $numberOfRectanglesToPaint ) { my ( $sx, $sy ); for ( 1 .. 200 ) { $sx = int( rand($W) ); $sy = int( rand($H) ); last if $canvas{"$sx,$sy"} eq 'white'; } my $color = $fillcolors[ rand @fillcolors ]; my @stack = ("$sx,$sy"); while (@stack) { my $pt = pop @stack; next if $seen{$pt}++; my ( $x, $y ) = split /,/, $pt; $canvas{$pt} = $color; $seen{$pt}++; for my $d ( [ -1, 0 ], [ 1, 0 ], [ 0, -1 ], [ 0, 1 ] ) { my ( $nx, $ny ) = ( $x + $d->[0], $y + $d->[1] ); next if $nx < 0 || $ny < 0 || $nx >= $W || $ny >= $H; my $k = "$nx,$ny"; push @stack, $k if $canvas{$k} eq 'white'; } }}return 1; }
And that’s the end of sub generate. I’ll return 1 at the end, just for tidiness’ sake. At that point, the object now has a well-defined canvas that should look somewhat like a Mondrian painting. Now we need an output method. Nothing fancy here, but Imager will let you output either jpg or png, by just specifying the filename you want to use.
sub save_png_or_jpg { my ( $self, $file ) = @_; my $scale = $self->scale_px; my $W = $self->width; my $H = $self->height; my %canvas = %{ $self->canvas }; my $img = Imager->new( xsize => $W * $scale, ysize => $H * $scale, channels => 3 ); for my $k ( keys %canvas ) { my ( $x, $y ) = split /,/, $k; my $rgb = $self->palette->{ $canvas{$k} }; my $color = Imager::Color->new(@$rgb); $img->box( xmin => $x * $scale, ymin => $y * $scale, xmax => ( $x + 1 ) * $scale - 1, ymax => ( $y + 1 ) * $scale - 1, color => $color, filled => 1 ); } $img->write( file => $file ) or die $img->errstr;}
After that, I scribbled up a little script to generate a Mondrian-styled painting using the default behaviors, and have it output a JPG.
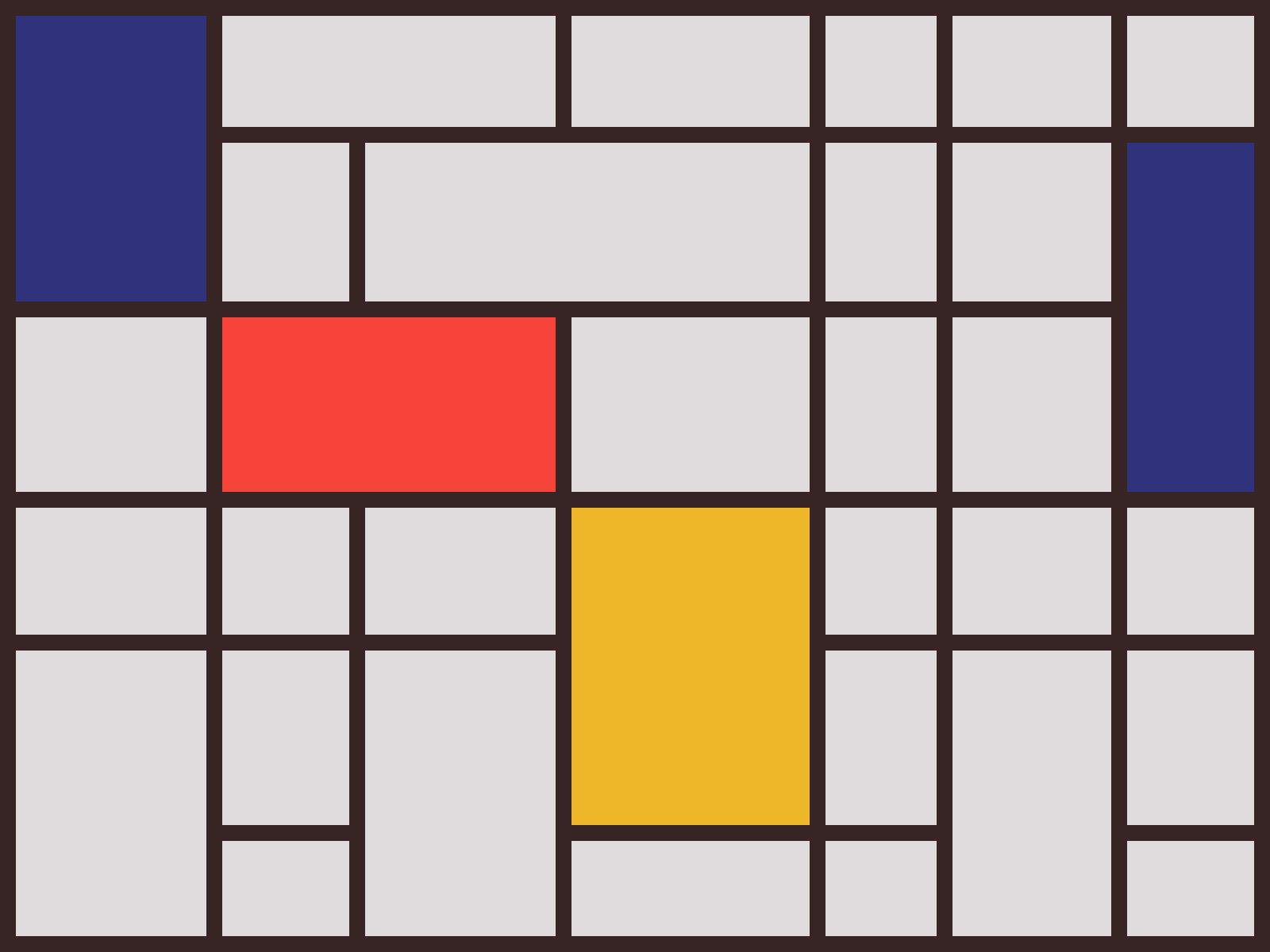
...and that’s how I started teaching art classes to Perl.
In the module I’ll be releasing to CPAN this holiday season (look for "Acme::Mondrian::Generator" in the next week or so, and I’ll be sure to update this to a link), I’ll also include a script to let you play around with the parameters of the generator, and output PNGs and SVGs as well as JPGs.
For completeness, here’s the whole Acme::Mondrian::Generator package after a bit of tidying-up:
package Acme::Mondrian::Generator;use strict;use warnings;use Moo;use Svg::Simple;use Imager;# Stuff the user can control on creation, with defaultshas resolution => ( is => 'ro', default => sub { return 80 } ); # width in cellshas aspect => ( is => 'ro', default => sub { return 0.75 } ); # height = width * aspecthas line_thickness => ( is => 'ro', default => sub { return 4 } ); # SVG black line thicknesshas scale_px => ( is => 'ro', default => sub { return 20 } ); # px per cell in PNG/SVGhas palette => ( is => 'ro', default => sub { return { # I used I<Tableau I> and an eyedropper tool for the web for these. white => [ 224, 220, 221 ], # lead white approximation black => [ 54, 37, 36 ], # bone + carbon black red => [ 246, 68, 58 ], # hematite / iron-oxide red yellow => [ 238, 184, 42 ], # mix: cadmium yellow / ochre / chrome yellow blue => [ 48, 50, 124 ], # dark blue }; });# Logical canvas (grid)has canvas => ( is => 'rw', default => sub { return {} } );has width => ( is => 'rw' ); # We'll calculate thesehas height => ( is => 'rw' );sub generate { my $self = shift; my $W = $self->resolution; my $H = int($self->resolution * $self->aspect); $self->width($W); $self->height($H); my %canvas; $self->canvas(\%canvas); # Initialize white grid for my $x (0..$W-1) { for my $y (0..$H-1) { $canvas{"$x,$y"} = 'white'; } } # Random thick grid lines like Mondrian my $min_x_gap = int($W/10); my $max_x_gap = int($W/5); my $min_y_gap = int($H/10); my $max_y_gap = int($H/5); my $numberOfSegmentsToDelete = 0; # Vertical lines my @vlines; { my $x = int( rand( $max_x_gap - $min_x_gap + 1 ) ) + $min_x_gap; while ( $x < $W - $min_x_gap ) { $numberOfSegmentsToDelete++; push @vlines, $x; for my $y ( 0 .. $H - 1 ) { $canvas{"$x,$y"} = 'black' } $x += int( rand( $max_x_gap - $min_x_gap + 1 ) ) + $min_x_gap; } } # Horizontal lines my @hlines; { my $y = int( rand( $max_y_gap - $min_y_gap + 1 ) ) + $min_y_gap; while ( $y < $H - $min_y_gap ) { push @hlines, $y; for my $x ( 0 .. $W - 1 ) { $canvas{"$x,$y"} = 'black' } $y += int( rand( $max_y_gap - $min_y_gap + 1 ) ) + $min_y_gap; } } my $numberOfRectanglesToPaint = $numberOfSegmentsToDelete - 2; $numberOfSegmentsToDelete = int($numberOfSegmentsToDelete * 1.5); # Delete segments for ( 1 .. $numberOfSegmentsToDelete ) { while (1) { # let's look for a black spot on the canvas. my $startx = int( rand( $W - 2 ) ) + 1; my $starty = int( rand( $H - 2 ) ) + 1; next if $canvas{"$startx,$starty"} eq 'white'; my $orientation; # Are we on a vertical line, or a horizontal if ( $canvas{ ( $startx - 1 ) . ",$starty" } eq 'white' && $canvas{ ( $startx + 1 ) . ",$starty" } eq 'white' ) { $orientation = 'vertical'; } elsif ( $canvas{ "$startx," . ( $starty - 1 ) } eq 'white' && $canvas{ "$startx," . ( $starty + 1 ) } eq 'white' ) { $orientation = 'horizontal'; } else { # We're at an intersection, so don't delete here. next; } my @points = ("$startx,$starty"); my $canDelete = 1; # Now find the collection of points on the rest of that segment, and push # them into @points. if ( $orientation eq 'vertical' ) { for my $dy ( -1, 1 ) { my $yy = $starty; while ( $yy > 0 && $yy < $H - 1 ) { $yy += $dy; my $l = $canvas{ ( $startx - 1 ) . ",$yy" }; my $r = $canvas{ ( $startx + 1 ) . ",$yy" }; if ( $l eq 'black' && $r eq 'black' ) { last; } elsif ( ( $l eq 'white' && $r eq 'black' ) || ( $l eq 'black' && $r eq 'white' ) ) { $canDelete = 0; last; } push @points, "$startx,$yy"; } last unless $canDelete; } } else { # horizontal for my $dx ( -1, 1 ) { my $xx = $startx; while ( $xx > 0 && $xx < $W - 1 ) { $xx += $dx; my $u = $canvas{ "$xx," . ( $starty - 1 ) }; my $d = $canvas{ "$xx," . ( $starty + 1 ) }; if ( $u eq 'black' && $d eq 'black' ) { last; } elsif ( ( $u eq 'white' && $d eq 'black' ) || ( $u eq 'black' && $d eq 'white' ) ) { $canDelete = 0; last; } push @points, "$xx,$starty"; } last unless $canDelete; } } next unless $canDelete; $canvas{$_} = 'white' for @points; last; } } # Border for my $xx (0..$W-1) { $canvas{"$xx,0"} = 'black'; $canvas{"$xx,".($H-1)} = 'black'; } for my $yy (0..$H-1) { $canvas{"0,$yy"} = 'black'; $canvas{($W-1).",$yy"} = 'black'; } # Flood fill rectangles my @fillcolors = qw(red yellow blue white white); # biased toward white my %seen; for ( 1 .. $numberOfRectanglesToPaint ) { my ( $sx, $sy ); for ( 1 .. 200 ) { $sx = int( rand($W) ); $sy = int( rand($H) ); last if $canvas{"$sx,$sy"} eq 'white'; } my $color = $fillcolors[ rand @fillcolors ]; my @stack = ("$sx,$sy"); while (@stack) { my $pt = pop @stack; # If our $color is 'white', this way we don't loop forever. next if $seen{$pt}++; my ( $x, $y ) = split /,/, $pt; $canvas{$pt} = $color; $seen{$pt}++; # If any adjacent points are white, push them in for coloring. for my $d ( [ -1, 0 ], [ 1, 0 ], [ 0, -1 ], [ 0, 1 ] ) { my ( $nx, $ny ) = ( $x + $d->[0], $y + $d->[1] ); next if $nx < 0 || $ny < 0 || $nx >= $W || $ny >= $H; my $k = "$nx,$ny"; push @stack, $k if $canvas{$k} eq 'white'; } } } return 1;}sub save_png_or_jpg { my ( $self, $file ) = @_; my $scale = $self->scale_px; my $W = $self->width; my $H = $self->height; my %canvas = %{ $self->canvas }; my $img = Imager->new( xsize => $W * $scale, ysize => $H * $scale, channels => 3 ); for my $k ( keys %canvas ) { my ( $x, $y ) = split /,/, $k; my $rgb = $self->palette->{ $canvas{$k} }; my $color = Imager::Color->new(@$rgb); $img->box( xmin => $x * $scale, ymin => $y * $scale, xmax => ( $x + 1 ) * $scale - 1, ymax => ( $y + 1 ) * $scale - 1, color => $color, filled => 1 ); } $img->write( file => $file ) or die $img->errstr;}1;
...and my little script to create one!
#!/usr/bin/env perluse strict;use warnings;use lib './lib';use Acme::Mondrian::Generator;my $gen = Acme::Mondrian::Generator->new();$gen->generate();my $f = "mondrian_".time().".jpg";$gen->save_png_or_jpg($f);
I hope this little bit of creativity inspires your own, whether in Perl, or on a canvas—or even in Raku or Python! Happy painting, and the happiest of holidays to you and the people you love, wherever they may be!