• “Never underestimate the powerful sums that arise when small numbers conspire.” *

• Zaryth Velmire

The Contest

Given a positive integer n, find n n-digit integers with distinct absolute values, the sum of whose n-th powers is non-zero but otherwise as close to zero as possible.

Example #1

For n = 3 you might choose the following three 3-digit numbers: (468, 126, -471). The sum of their cubes is (468)3 + (126)3 + (-471)3 = (102503232) + (2000276) + (-104487111) = 123.

Alternatively, you might choose (-665, -780, 916). The sum of the cubes is (-665)3 + (-780)3 + (916)3 = (-294079625) + (-474552000) + (768575296) = -529.

Of these two solutions, the first is better because 123 is closer to zero than is -529.

Example #2

The following are unbeatable solutions for n = 3 and n = 5:

• (172, -138, -135) => (172)3 + (-138)3 + (-135)3 = 1
• (-31919, -24271, 18410, 27764, 30965) => (-32919)5 + (-24271)5 + (18410)5 + (27764)5 + (30965)5 = -1

Why are these solutions unbeatable? Because there are no non-zero integers closer to zero than 1 and -1.

Example #3

The following solutions are not acceptable:

• (347, -216, -347) — because 347 and -347 have the same absolute value
• (13527, 42084, 55110, 66633, -72144) — because the sum of the 5th powers is zero

Which values of n?

The values of n for which you must find solutions are the 25 odd integers from 7 through 55.

Attribution

This contest was inspired by Shyam Sunder Gupta’s “Can You Find”, Problem #63.

The Scoring System

Each entry submitted to the contest receives an entry score equal to the base-10 logarithm of the absolute value of the sum of its n nth powers, plus 1. Algebraically, its entry score equals:

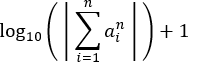
where the ai are the n-digit numbers in the entry.

Each time you submit an entry the system will compare it to your prior entries, if any, and will retain only your best entry for each of the 25 values of n. It will assign each of these 25 entries a subscore [see next paragraph] from 0 to 1 and the sum of your subscores will be your ** contest score **. The participant with the highest contest score wins.

The system computes the subscore for an individual entry as follows. If the entry is the best entry submitted for that n by anyone, the subscore is 1 point; otherwise the subscore is only a fraction of a point. The fraction is the smallest entry score by anyone for that n, divided by your entry score. For example, suppose your entry for n = 7 has an entry score of 500. Further suppose that the best entry submitted to the contest for n = 7 has an entry score of 200. Then your subscore for n = 7 is 200 / 500 = 0.4.

How to Enter

Paste your solutions into the appropriate box on the Submit page and click Submit Entry.

Express each solution as a comma-delimited list of n signed n-digit values. To submit more than one solution at a time, separate solutions with semicolons. Do not place a semicolon after the last solution.

For example, to submit these solutions:

• (172, -138, -135) => 1723 - 1383 - 1353 = 1

• (32919, 24271, -18410, -27764, -30965) => 329195 + 242715 - 184105 - 277645 - 309655 = 1

you would submit:

172, -138, -135; 32919, 24271, -18410, -27764, -30965

Include spaces and other white space (tabs, line breaks, etc.) anywhere you like – but not, of course, within a number.

You are not permitted to submit a solution unless it improves on your previous submissions for that n. However, for debugging purposes, you may submit whatever solutions for n = 1, 3 and 5 you wish — the system validates them and gives you their scores, as it does for all submissions, but does not store them in the database.

Getting Your Questions Answered

First, check the FAQ section below. If you can’t find the information you need there, send your question to the AZsPCs Forum. If your question is of a personal nature, and not of general interest, send an email directly to Al Zimmermann.

The AZsPCs Forum

If you think you might enter the contest, you should join the AZsPCs Forum. You can join either by sending a blank email here or by visiting the forum on groups.io. The AZsPCs Forum serves two purposes. First, it allows contestants to ask for clarifications to the rules. Be aware that sometimes these requests result in changes to the rules, and the first place those changes are announced is in the AZsPCs Forum. Second, the Forum allows contestants to interact with each other regarding programming techniques, results and anything else relevant to the contest.

Frequently Asked Questions

May I get help from an AI?

Yes.

Can teams enter the contest?

Yes. But a team can only be formed by those who have not already entered the contest as individuals. Once you enter as an individual, team membership is no longer open to you. Likewise, once you’ve joined a team you can’t resign from it and start submitting entries on your own behalf.

If you would like to form a team, please follow these instructions:

• If they do not already exist, create individual accounts for each team member. Do not create a second account for any team member who already has one.

• Let me know each team member’s name and registered email address. It is important that no team member submit any entries to this contest until I notify you that the team has been created.

• After I’ve created the team, team members can submit entries to the contest from their individual accounts. The contest engine automatically merges these entries when it creates the standings page.

• Unless you are satisfied with the defaults, also let me know what team name and team location you would like to use on the standings page. Note that if all team members are from the same organization, the organization name can be included in the location, e.g., “Olaf Academy, Oslo, Norway”. – For team name, the default is a combination of your individual names. For example, “Newton / Leibniz” or “Moe / Larry / Curly”. – For team location, there’s no rule – I use whatever seems reasonable.

Note: Teams are contest-specific. Joining a team for this contest does not affect your participation in other contests.

May I write a program that submits entries by bypassing my browser?

Yes.

May I programmatically download the standings page at regular intervals? How frequently would be reasonable?

Yes, you may programmatically download the standings page at regular intervals. Please feel free to download it as often as once per second. If you want to download the standings page more frequently than that, please contact me first.

I’ve written a little program that helps a person generate solutions manually. May I distribute the executable to other contestants?

No. This is a programming contest and writing useful tools is something one should be able to do for oneself. That alone would be sufficient reason to disallow the distribution of such tools, but consider also that you would be disadvantaging those who either don’t hear about your tool (not everyone joins the forum) or can’t run your executable in their environment.

However, if you are part of a team, you may share such tools with your teammates.

What topics are appropriate for the AZsPCs Forum?

With only one exception, if it’s related to AZsPCs then it’s fine to talk about it in the AZsPCs Forum. The exception is spoilers. Spoilers include:

• specific solutions
• detailed algorithms (yes, detailedness is subjective)

If you are not sure if something would be considered a spoiler, ask me.

What happens if I submit a solution for n = 1 or n = 3 or n = 5?

You can use n = 1 and n = 3 and n = 5 for debugging. When you submit a solution for one of these “forbidden” values of n, it goes through the same validation process as other solutions. If it fails, you get an error message. If it passes, you see its score, but the solution will not be stored in the database. You may submit the same solutions for n = 1, 3 and 5 repeatedly.

To what extent does this site adhere to U.S. and EU privacy regulations and practices for commercial websites?

Al Zimmermann’s Programming Contests is not a commercial website and your privacy is not protected by laws that apply specifically to commercial websites. Nevertheless, your email address and other personal data are never shared with third parties.

• If you do not want your data in this website’s database, do not register.

• If you do not want your name to appear on this website, do not enter its contests.