The standard Lanczos method for computing matrix functions has a brutal memory requirement: storing an n×kn \times k basis matrix that grows with every iteration. For a 500.000500.000-variable problem needing 10001000 iterations, that’s roughly 4 GB just for the basis.
In this post, we will explore one of the most straightforward solutions to this problem: a two-pass variant of the Lanczos algorithm that only requires O(n)O(n) memory at the cost of doubling the number of matrix-vector products. The surprising part is that when implemented carefully, the two-pass version isn’t just memory-efficient—it can be faster for certain problems. We will dig into why.
- All code is available on GitHub: two-pass-lanczos
- The full technical…
The standard Lanczos method for computing matrix functions has a brutal memory requirement: storing an n×kn \times k basis matrix that grows with every iteration. For a 500.000500.000-variable problem needing 10001000 iterations, that’s roughly 4 GB just for the basis.
In this post, we will explore one of the most straightforward solutions to this problem: a two-pass variant of the Lanczos algorithm that only requires O(n)O(n) memory at the cost of doubling the number of matrix-vector products. The surprising part is that when implemented carefully, the two-pass version isn’t just memory-efficient—it can be faster for certain problems. We will dig into why.
- All code is available on GitHub: two-pass-lanczos
- The full technical report with proofs and additional experiments: report.pdf
Table of Contents
Open Table of Contents
Computing Matrix Functions
Let’s consider the problem of computing the action of matrix functions on a vector:
x=f(A)b\mathbf{x} = f(\mathbf{A})\mathbf{b}
where A\mathbf{A} is a large sparse Hermitian matrix and ff is a matrix function defined on the spectrum of A\mathbf{A}. This is a problem that appears pretty often in scientific computing: solving linear systems corresponds to f(z)=z−1f(z) = z^{-1}, exponential integrators for PDEs use f(z)=exp(tz)f(z) = \exp(tz), and many other problems require functions like f(z)=z−1/2f(z) = z^{-1/2} or f(z)=sign(z)f(z) = \text{sign}(z).
Indeed, there are a lot problems with computing f(A)f(\mathbf{A}) directly. First of all, even if A\mathbf{A} is sparse, f(A)f(\mathbf{A}) is generally dense. Storing it explicitly is out of the question for large problems. Even if we could store it, computing it directly would require algorithms like the Schur-Parlett method that scale as O(n3)O(n^3), which is impractical for large nn.
However we know that given any matrix function ff defined on the spectrum of A\mathbf{A}, we can express f(A)f(\mathbf{A}) as a polynomial in A\mathbf{A} of degree at most nn (the size of the matrix) such that f(A)=pn(A)f(\mathbf{A}) = p_{n}(\mathbf{A}) (this is a consequence of the Cayley-Hamilton theorem). This polynomial interpolates ff and its derivatives in the Hermitian sense at the eigenvalues of A\mathbf{A}.
This gives us a good and a bad news: the good news is that, well, we can express f(A)f(\mathbf{A}) as a polynomial in A\mathbf{A}. The bad news is that the degree of this polynomial can be as high as nn, which is huge for large problems. The idea is then to find a low-degree polynomial approximation to ff that is good enough for our purposes. If we can find a polynomial pkp_k of degree k≪nk \ll n such that pk(A)≈f(A)p_k(\mathbf{A}) \approx f(\mathbf{A}), then we can approximate the solution as:
f(A)b≈pk(A)b=∑i=0kciAibf(\mathbf{A})\mathbf{b} \approx p_k(\mathbf{A})\mathbf{b} = \sum_{i=0}^k c_i \mathbf{A}^i \mathbf{b}
This polynomial only involves vectors within a specific subspace.
Krylov Projection
We can notice that pk(A)bp_k(\mathbf{A})\mathbf{b} only depends on vectors in the Krylov subspace of order kk
Kk(A,b)=span{b,Ab,A2b,…,Ak−1b}\mathcal{K}_k(\mathbf{A}, \mathbf{b}) = \text{span}{\mathbf{b}, \mathbf{Ab}, \mathbf{A}2\mathbf{b}, \ldots, \mathbf{A}{k-1}\mathbf{b}}
This is fortunate: we can compute an approximate solution by staying within this space, which only requires repeated matrix-vector products with A\mathbf{A}. For large sparse matrices, that’s the only operation we can do efficiently anyway.
We don’t need to construct Aj\mathbf{A}j explicitly. We compute iteratively: A(Aj−1b)\mathbf{A}(\mathbf{A}{j-1}\mathbf{b}).
But there’s a problem: the raw vectors {Ajb}{\mathbf{A}^j\mathbf{b}} form a terrible basis. They quickly become nearly parallel, making any computation numerically unstable. We need an orthonormal basis.
Building an Orthonormal Basis
The standard method is the Arnoldi process, which is Gram-Schmidt applied to Krylov subspaces. We start by normalizing v1=b/∥b∥2\mathbf{v}_1 = \mathbf{b} / |\mathbf{b}|_2. Then, iteratively:
-
Compute a new candidate: wj=Avj\mathbf{w}_j = \mathbf{A}\mathbf{v}_j
-
Orthogonalize against all existing basis vectors: v~j=wj−∑i=1j(viHwj)vi\tilde{\mathbf{v}}_j = \mathbf{w}_j - \sum_{i=1}^j (\mathbf{v}_i^H \mathbf{w}_j) \mathbf{v}_i
-
Normalize: vj+1=v~j/∥v~j∥2\mathbf{v}_{j+1} = \tilde{\mathbf{v}}_j / |\tilde{\mathbf{v}}_j|_2
The coefficients hij=viHwjh_{ij} = \mathbf{v}_i^H \mathbf{w}_j become entries of a projected matrix. After kk iterations, we have:
- Vk=[v1,…,vk]\mathbf{V}_k = [\mathbf{v}_1, \ldots, \mathbf{v}_k]: an orthonormal basis for Kk(A,b)\mathcal{K}_k(\mathbf{A}, \mathbf{b})
- Hk\mathbf{H}_k: an upper Hessenberg matrix representing the projection of A\mathbf{A} onto this subspace
We can express this relationship with the Arnoldi decomposition:
AVk=VkHk+hk+1,kvk+1ekT\mathbf{A}\mathbf{V}_k = \mathbf{V}_k \mathbf{H}_k + h_{k+1,k} \mathbf{v}_{k+1} \mathbf{e}_k^T
Solving in the Reduced Space
Now we approximate our original problem by solving it in the small kk-dimensional space. Using the Full Orthogonal Method (FOM), we enforce that the residual is orthogonal to the Krylov subspace. This gives:
xk=Vkyk\mathbf{x}_k = \mathbf{V}_k \mathbf{y}_k
where yk\mathbf{y}_k is computed as:
yk=f(Hk)e1∥b∥2\mathbf{y}_k = f(\mathbf{H}_k) \mathbf{e}_1 |\mathbf{b}|_2
The heavy lifting is now on computing f(Hk)f(\mathbf{H}_k), a small k×kk \times k matrix. Since k≪nk \ll n, we can afford direct methods like Schur-Parlett (O(k3)O(k^3)).
For f(z)=z−1f(z) = z^{-1} (linear systems), this reduces to solving Hkyk=e1∥b∥2\mathbf{H}_k \mathbf{y}_k = \mathbf{e}_1 |\mathbf{b}|_2 with LU decomposition.
The Lanczos Algorithm
When A\mathbf{A} is Hermitian (or symmetric in the real case), the general Arnoldi process simplifies dramatically. We can prove that Hk=VkHAVk\mathbf{H}_k = \mathbf{V}_k^H \mathbf{A} \mathbf{V}_k must also be Hermitian. A matrix that is both upper Hessenberg and Hermitian must be real, symmetric, and tridiagonal. This is a huge simplification.
In the literature, this projected matrix is denoted Tk\mathbf{T}_k to highlight its tridiagonal structure:
Tk=(α1β1β1α2β2β2⋱⋱⋱αk)\mathbf{T}_k = \begin{pmatrix} \alpha_1 & \beta_1 & & \ \beta_1 & \alpha_2 & \beta_2 & \ & \beta_2 & \ddots & \ddots \ & & \ddots & \alpha_k \end{pmatrix}
where αj∈R\alpha_j \in \mathbb{R} are the diagonal elements and βj∈R\beta_j \in \mathbb{R} are the off-diagonals (subdiagonals from the orthogonalization).
Three-Term Recurrence
This tridiagonal structure leads to a beautiful simplification. To build the next basis vector vj+1\mathbf{v}_{j+1}, we don’t need the entire history of vectors. We only need the two previous ones. Since A\mathbf{A} is Hermitian, this guarantees that any new vector is automatically orthogonal to all earlier vectors (beyond the previous two). So we can skip the full orthogonalization and use a simple three-term recurrence:
Avj=βj−1vj−1+αjvj+βjvj+1\mathbf{A}\mathbf{v}_j = \beta_{j-1}\mathbf{v}_{j-1} + \alpha_j \mathbf{v}_j + \beta_j \mathbf{v}_{j+1}
Rearranging gives us an algorithm to compute vj+1\mathbf{v}_{j+1} directly:
-
Compute the candidate: wj+1=Avjw_{j+1} = \mathbf{A}\mathbf{v}_j
-
Extract the diagonal coefficient: αj=vjHwj+1\alpha_j = \mathbf{v}_j^H w_{j+1}
-
Orthogonalize against the two previous vectors: v~j+1=wj+1−αjvj−βj−1vj−1\tilde{\mathbf{v}}_{j+1} = w_{j+1} - \alpha_j \mathbf{v}_j - \beta_{j-1}\mathbf{v}_{j-1}
-
Normalize: βj=∥v~j+1∥2\beta_j = |\tilde{\mathbf{v}}_{j+1}|_2 and vj+1=v~j+1/βj\mathbf{v}_{j+1} = \tilde{\mathbf{v}}_{j+1} / \beta_j
This is known as the Lanczos algorithm. It’s more efficient than Arnoldi because each iteration only orthogonalizes against two previous vectors instead of all prior ones.
Reconstructing the Solution
After kk iterations, we end up with the tridiagonal matrix Tk\mathbf{T}_k and all kk basis vectors Vk=[v1,…,vk]\mathbf{V}_k = [\mathbf{v}_1, \ldots, \mathbf{v}_k]. We can then reconstruct the approximate solution as:
xk=Vkyk\mathbf{x}_k = \mathbf{V}_k \mathbf{y}_k
where yk=f(Tk)e1∥b∥2\mathbf{y}_k = f(\mathbf{T}_k) \mathbf{e}_1 |\mathbf{b}|_2 is solved from the small tridiagonal matrix.
There is a timing problem however: we cannot compute the coefficients yk\mathbf{y}_k until all kk iterations are complete. The full matrix Tk\mathbf{T}_k is only available at the end, so we must store every basis vector vj\mathbf{v}_j along the way, leading to a memory cost of O(nk)O(nk).
So we’re left with a choice: whether we store all the basis vectors and solve the problem in kk passes, or find a way to avoid storing them. There is a middle ground.
There are also techniques to compress the basis vectors, have a look here
Two-Pass Algorithm
Here’s where we break the timing deadlock. The insight that we don’t actually need to store the basis vectors if we can afford to compute them twice
Think about what we have after the first pass. We’ve computed all the αj\alpha_j and βj\beta_j coefficients that compose the entire tridiagonal matrix Tk\mathbf{T}_k. These numbers are small compared to the full basis. What if we kept only these scalars, discarded all the vectors, and then replayed the Lanczos recurrence a second time? We’d regenerate the same basis, and this time we’d use it to build the solution.
This comes at a cost. We run Lanczos twice, so we pay for 2k2k matrix-vector products instead of kk. But we only ever store a constant number of vectors in memory, no O(nk)O(nk) basis matrix. The memory complexity drops to O(n)O(n).
It sounds like a bad trade at first. But as we’ll see later, the cache behavior of this two-pass approach can actually make it as fast (or even faster) on real hardware if well optimized.
First Pass: Compute the Projected Problem
We initialize v1=b/∥b∥2\mathbf{v}_1 = \mathbf{b} / |\mathbf{b}|_2 and set β0=0\beta_0 = 0, v0=0\mathbf{v}_0 = \mathbf{0}.Then we run the standard Lanczos recurrence:
wj=Avjw_j = \mathbf{A}\mathbf{v}_j αj=vjHwj\alpha_j = \mathbf{v}_j^H w_j v~j+1=wj−αjvj−βj−1vj−1\tilde{\mathbf{v}}_{j+1} = w_j - \alpha_j \mathbf{v}_j - \beta_{j-1}\mathbf{v}_{j-1} βj=∥v~j+1∥2,vj+1=v~j+1/βj\beta_j = |\tilde{\mathbf{v}}_{j+1}|_2, \quad \mathbf{v}_{j+1} = \tilde{\mathbf{v}}_{j+1} / \beta_j
At each step, we record αj\alpha_j and βj\beta_j. But we do not store vj\mathbf{v}_j. Instead, we discard it immediately after computing vj+1\mathbf{v}_{j+1}. In this way we only keep in memory at most just three vectors at any time (vj−1\mathbf{v}_{j-1}, vj\mathbf{v}_j, and the working vector wjw_j).
After kk iterations, we have the full set {α1,β1,…,αk,βk}{\alpha_1, \beta_1, \ldots, \alpha_k, \beta_k}. These O(k)O(k) scalars define the tridiagonal matrix Tk\mathbf{T}_k. We can now solve:
yk=f(Tk)e1∥b∥2\mathbf{y}_k = f(\mathbf{T}_k) \mathbf{e}_1 |\mathbf{b}|_2
This is the solution in the reduced space. Now that we have the coefficients we need to build xk\mathbf{x}_k.
Second Pass: Reconstruct and Accumulate
With yk\mathbf{y}_k in memory, we replay the Lanczos recurrence exactly as before. We start with the same initialization (v1\mathbf{v}_1, β0\beta_0, v0\mathbf{v}_0) and apply the same sequence of operations, using the stored scalars αj\alpha_j and βj\beta_j to reconstruct each basis vector on demand. We can write some rust-like pseudocode for this second pass to get a feel for it:
let mut x_k = vec![0.0; n];
let mut v_prev = vec![0.0; n];
let mut v_curr = b.clone() / b_norm;
for j in 1..=k {
let w = A @ v_curr; // Matrix-vector product
// We don't recompute alpha/beta; we already have them from pass 1
let alpha_j = alphas[j - 1];
let beta_prev = j > 1 ? betas[j - 2] : 0.0;
// Accumulate the solution
x_k += y_k[j - 1] * v_curr;
// Regenerate the next basis vector for the *next* iteration
let v_next = (w - alpha_j * v_curr - beta_prev * v_prev) / betas[j - 1];
// Slide the window forward
v_prev = v_curr;
v_curr = v_next;
}
This loop regenerates each vj\mathbf{v}_j on demand and immediately uses it to update the solution. Once we’ve accumulated (yk)jvj(\mathbf{y}_k)_j \mathbf{v}_j into xk\mathbf{x}_k, we discard the vector. We never store the full basis.
A Subtle Numerical Point
There is one detail worth noting: floating-point arithmetic is deterministic. When we replay the Lanczos recurrence in the second pass with the exact same inputs and the exact same order of operations, we get bitwise-identical vectors. The vj\mathbf{v}_j regenerated in pass 2 are identical to the ones computed in pass 1.
However, the order in which we accumulate the solution differs. In a standard Lanczos, xk\mathbf{x}_k is built as a single matrix-vector product: xk=Vkyk\mathbf{x}_k = \mathbf{V}_k \mathbf{y}_k (a gemv call in BLAS). In the two-pass method, it’s built as a loop of scaled vector additions (a series of axpy calls). These operations accumulate rounding error differently, so the final solution differs slightly, typically by machine epsilon. This rarely matters in practice, and convergence is unaffected.
Implementation
Building this in Rust forces us to think concretely about where data lives and how it flows through the cache hierarchy. We need to control memory layout, decide when allocations happen, and choose abstractions that cost us nothing at runtime.
For linear algebra, we reach for faer. Three design choices in this library matter for what we’re building:
- Stack allocation via
MemStack: Pre-allocated scratch space that lives for the entire computation. The hot path becomes allocation-free. - Matrix-free operators: The
LinOptrait defines an operator by its action (apply) without materializing a matrix. For large sparse problems, this is the only viable approach. - SIMD-friendly loops: The
zip!macro generates code that compiles to packed instructions.
Recurrence Step
Our starting point is the Lanczos three-term recurrence that we derived earlier:
βjvj+1=Avj−αjvj−βj−1vj−1\beta_j \mathbf{v}_{j+1} = \mathbf{A}\mathbf{v}_j - \alpha_j \mathbf{v}_j - \beta_{j-1}\mathbf{v}_{j-1}
We can translate this into a recurrence step function. The signature looks like this:
fn lanczos_recurrence_step<T: ComplexField, O: LinOp<T>>(
operator: &O,
mut w: MatMut<'_, T>,
v_curr: MatRef<'_, T>,
v_prev: MatRef<'_, T>,
beta_prev: T::Real,
stack: &mut MemStack,
) -> (T::Real, Option<T::Real>)
The function is generic over the field type T (f64, c64, etc.) and the operator type O. It operates on matrix views (MatMut and MatRef) to avoid unnecessary data copies. The return type gives us the diagonal element αj\alpha_j and, if no breakdown occurs, the off-diagonal βj\beta_j.
Now we can implement the body by following the math. The first step is the most expensive:
// 1. Apply operator: w = A * v_curr
operator.apply(w.rb_mut(), v_curr, Par::Seq, stack);
The matrix-vector product dominates the computational cost. Everything else is secondary.
Next, we orthogonalize against vj−1\mathbf{v}_{j-1}. This is where we benefit from faer’s design. The zip! macro fuses this operation into a single loop that the compiler vectorizes into SIMD instructions.
// 2. Orthogonalize against v_{j-1}: w -= β_{j-1} * v_{j-1}
let beta_prev_scaled = T::from_real_impl(&beta_prev);
zip!(w.rb_mut(), v_prev).for_each(|unzip!(w_i, v_prev_i)| {
*w_i = sub(w_i, &mul(&beta_prev_scaled, v_prev_i));
});
With w partially orthogonalized, we can compute the diagonal coefficient via an inner product. Since A\mathbf{A} is Hermitian, αj\alpha_j is guaranteed real.
// 3. Compute α_j = v_j^H * w
let alpha = T::real_part_impl(&(v_curr.adjoint() * w.rb())[(0, 0)]);
We complete the orthogonalization against vj\mathbf{v}_j with another zip! loop.
// 4. Orthogonalize against v_j: w -= α_j * v_j
let alpha_scaled = T::from_real_impl(&alpha);
zip!(w.rb_mut(), v_curr).for_each(|unzip!(w_i, v_curr_i)| {
*w_i = sub(w_i, &mul(&alpha_scaled, v_curr_i));
});
Now w holds the unnormalized next basis vector. We compute its norm to get βj\beta_j. If this norm is numerically zero, the Krylov subspace is invariant, the iteration has reached its natural stopping point. This is called breakdown.
// 5. Compute β_j = ||w||_2 and check for breakdown
let beta = w.rb().norm_l2();
let tolerance = breakdown_tolerance::<T::Real>();
if beta <= tolerance {
(alpha, None)
} else {
(alpha, Some(beta))
}
The function returns None for βj\beta_j when breakdown occurs, signaling to the caller that no further iterations should proceed.
An Iterator for State Management
The recurrence step is a pure function, but calling it in a loop is both inefficient and awkward. We’d need to manually pass vectors in and out of each iteration. More critically, we’d create copies when we should be reusing memory.
The iterator pattern solves this. We create a struct that encapsulates the state:
struct LanczosIteration<'a, T: ComplexField, O: LinOp<T>> {
operator: &'a O,
v_prev: Mat<T>, // v_{j-1}
v_curr: Mat<T>, // v_j
work: Mat<T>, // Workspace for the next vector
beta_prev: T::Real, // β_{j-1}
// ... iteration counters
}
The main design choice here is that vectors are owned (Mat<T>), not borrowed. This enables an optimization in the next_step method. After computing the next vector and normalizing it into work, we cycle the state without allocating or copying:
// Inside next_step, after normalization...
core::mem::swap(&mut self.v_prev, &mut self.v_curr);
core::mem::swap(&mut self.v_curr, &mut self.work);
On x86-64, swapping two Mat<T> structures (fat pointers) compiles to three mov instructions. The pointers change, but no vector data moves. After the swap, v_prev points to what v_curr held, v_curr points to work’s allocation, and work points to the old v_prev data. In the next iteration, work gets reused.
We keep exactly three n-dimensional vectors live in memory. The same allocations cycle through the computation, staying hot in L1 cache. This is the core reason the two-pass method can be faster than expected, the working set never leaves cache.
First Pass: Computing the Decomposition
The first pass runs the Lanczos iteration and collects the coefficients {αj,βj}{\alpha_j, \beta_j}. Basis vectors are discarded after each step.
pub fn lanczos_pass_one<T: ComplexField>(
operator: &impl LinOp<T>,
b: MatRef<'_, T>,
k: usize,
stack: &mut MemStack,
) -> Result<LanczosDecomposition<T::Real>, LanczosError> {
// ...
}
We allocate vectors for the coefficients with a capacity hint to avoid reallocations:
let mut alphas = Vec::with_capacity(k);
let mut betas = Vec::with_capacity(k - 1);
Then we construct the iterator. This allocates the three work vectors once. After this point, the hot path is allocation-free:
let mut lanczos_iter = LanczosIteration::new(operator, b, k, b_norm)?;
for i in 0..k {
if let Some(step) = lanczos_iter.next_step(stack) {
alphas.push(step.alpha);
steps_taken += 1;
let tolerance = breakdown_tolerance::<T::Real>();
if step.beta <= tolerance {
break;
}
if i < k - 1 {
betas.push(step.beta);
}
} else {
break;
}
}
The check for breakdown stops the iteration when the residual becomes numerically zero. This means we’ve found an invariant subspace and there’s no value in continuing.
At the end, we collect the scalars into a LanczosDecomposition struct. The memory footprint throughout this pass is constant: three n-dimensional vectors plus two small arrays that grow to at most kk elements.
Second Pass: Reconstructing the Solution
Now we face a different problem. We have the {αj,βj}{\alpha_j, \beta_j} coefficients from the first pass and the coefficient vector yk=f(Tk)e1∥b∥2\mathbf{y}_k = f(\mathbf{T}_k) \mathbf{e}_1 |\mathbf{b}|_2 from solving the projected problem. We need to reconstruct the solution:
xk=∑j=1k(yk)jvj\mathbf{x}_k = \sum_{j=1}^k (\mathbf{y}_k)_j \mathbf{v}_j
without storing the full basis matrix Vk\mathbf{V}_k.
The recurrence step in this pass is structurally similar to the first pass, but with a key difference: we no longer compute inner products or norms. We already know the coefficients, so the step becomes pure reconstruction.
fn lanczos_reconstruction_step<T: ComplexField, O: LinOp<T>>(
operator: &O,
mut w: MatMut<'_, T>,
v_curr: MatRef<'_, T>,
v_prev: MatRef<'_, T>,
alpha_j: T::Real,
beta_prev: T::Real,
stack: &mut MemStack,
) {
// Apply operator
operator.apply(w.rb_mut(), v_curr, Par::Seq, stack);
// Orthogonalize using stored α_j and β_{j-1}
let beta_prev_scaled = T::from_real_impl(&beta_prev);
zip!(w.rb_mut(), v_prev).for_each(|unzip!(w_i, v_prev_i)| {
*w_i = sub(w_i, &mul(&beta_prev_scaled, v_prev_i));
});
let alpha_scaled = T::from_real_impl(&alpha_j);
zip!(w.rb_mut(), v_curr).for_each(|unzip!(w_i, v_curr_i)| {
*w_i = sub(w_i, &mul(&alpha_scaled, v_curr_i));
});
}
This is cheaper than the first-pass recurrence. We’ve eliminated the inner products that computed αj\alpha_j and the norm calculation for βj\beta_j. What remains is pure orthogonalization and the operator application.
lanczos_pass_two implements this reconstruction. We initialize the three work vectors and the solution accumulator:
pub fn lanczos_pass_two<T: ComplexField>(
operator: &impl LinOp<T>,
b: MatRef<'_, T>,
decomposition: &LanczosDecomposition<T::Real>,
y_k: MatRef<'_, T>,
stack: &mut MemStack,
) -> Result<Mat<T>, LanczosError> {
let mut v_prev = Mat::<T>::zeros(b.nrows(), 1);
let inv_norm = T::from_real_impl(&T::Real::recip_impl(&decomposition.b_norm));
let mut v_curr = b * Scale(inv_norm); // v_1
let mut work = Mat::<T>::zeros(b.nrows(), 1);
// Initialize solution with first component
let mut x_k = &v_curr * Scale(T::copy_impl(&y_k[(0, 0)]));
We build the solution incrementally by starting with the first basis vector scaled by its coefficient. The main loop then regenerates each subsequent vector: we regenerate each subsequent basis vector, normalize it using the stored βj\beta_j, and immediately accumulate its contribution:
for j in 0..decomposition.steps_taken - 1 {
let alpha_j = T::Real::copy_impl(&decomposition.alphas[j]);
let beta_j = T::Real::copy_impl(&decomposition.betas[j]);
let beta_prev = if j == 0 {
T::Real::zero_impl()
} else {
T::Real::copy_impl(&decomposition.betas[j - 1])
};
// 1. Regenerate the unnormalized next vector
lanczos_reconstruction_step(
operator,
work.as_mut(),
v_curr.as_ref(),
v_prev.as_ref(),
alpha_j,
beta_prev,
stack,
);
// 2. Normalize using stored β_j
let inv_beta = T::from_real_impl(&T::Real::recip_impl(&beta_j));
zip!(work.as_mut()).for_each(|unzip!(w_i)| {
*w_i = mul(w_i, &inv_beta);
});
// 3. Accumulate: x_k += y_{j+1} * v_{j+1}
let coeff = T::copy_impl(&y_k[(j + 1, 0)]);
zip!(x_k.as_mut(), work.as_ref()).for_each(|unzip!(x_i, v_i)| {
*x_i = add(x_i, &mul(&coeff, v_i));
});
// 4. Cycle vectors for the next iteration
core::mem::swap(&mut v_prev, &mut v_curr);
core::mem::swap(&mut v_curr, &mut work);
}
The accumulation x_k += y_{j+1} * v_{j+1} is implemented as a fused multiply-add in the zip! loop. On hardware with FMA support, this becomes a single instruction per element, not three separate operations.
Note that we accumulate the solution incrementally. After each iteration, x_k contains a partial result. We cycle through the same three vectors (v_prev, v_curr, work), keeping the working set small and resident in L1 cache.
Compare this to the standard method’s final reconstruction step: xk=Vkyk\mathbf{x}_k = \mathbf{V}_k \mathbf{y}_k. This is a dense matrix-vector product where Vk\mathbf{V}_k is n×kn \times k. When nn and kk are both large, this matrix no longer fits in cache. The CPU must stream it from main memory, paying the cost of memory latency. Each element requires a load, multiply, and accumulate, but the load operations dominate—the CPU stalls waiting for data.
In our two-pass reconstruction, the operator $\mathbf{A}$ is applied kk times, but against vectors that stay in cache. The memory bandwidth is spent on reading the sparse structure of A\mathbf{A} and the vector elements, not on scanning a dense n×kn \times k matrix.
This is the reason the two-pass method can be faster on real hardware despite performing twice as many matrix-vector products. The cache behavior of the reconstruction phase overwhelms the savings of storing the basis.
The Public API
We can wrap the two passes into a single entry point:
pub fn lanczos_two_pass<T, O, F>(
operator: &O,
b: MatRef<'_, T>,
k: usize,
stack: &mut MemStack,
mut f_tk_solver: F,
) -> Result<Mat<T>, LanczosError>
where
T: ComplexField,
O: LinOp<T>,
F: FnMut(&[T::Real], &[T::Real]) -> Result<Mat<T>, anyhow::Error>,
{
// First pass: compute T_k coefficients
let decomposition = lanczos_pass_one(operator, b, k, stack)?;
if decomposition.steps_taken == 0 {
return Ok(Mat::zeros(b.nrows(), 1));
}
// Solve projected problem: y_k' = f(T_k) * e_1
let y_k_prime = f_tk_solver(&decomposition.alphas, &decomposition.betas)?;
// Scale by ||b||
let y_k = &y_k_prime * Scale(T::from_real_impl(&decomposition.b_norm));
// Second pass: reconstruct solution
lanczos_pass_two(operator, b, &decomposition, y_k.as_ref(), stack)
}
The design separates concerns. The f_tk_solver closure is where we inject the specific matrix function. We compute the Lanczos decomposition, then pass the coefficients to the user-provided solver, which computes yk′=f(Tk)e1\mathbf{y}_k’ = f(\mathbf{T}_k) \mathbf{e}_1 for whatever function ff is needed. This decoupling means we handle linear solves, matrix exponentials, or any other function without modifying the core algorithm.
The caller provides f_tk_solver as a closure. It receives the raw {αj,βj}{\alpha_j, \beta_j} arrays and must return the coefficient vector yk′\mathbf{y}_k’. We then scale it by ∥b∥2|\mathbf{b}|_2 and pass everything to the second pass.
Example: Solving a Linear System
To see this in practice, consider solving Ax=b\mathbf{Ax} = \mathbf{b}. We compute f(z)=z−1f(z) = z^{-1}, which means the f_tk_solver must solve the small tridiagonal system Tky′=e1\mathbf{T}_k \mathbf{y}’ = \mathbf{e}_1.
Since Tk\mathbf{T}_k is tridiagonal, we can exploit its structure. A sparse LU factorization solves it in O(k)O(k) time instead of the O(k3)O(k^3) cost of a dense method.
let f_tk_solver = |alphas: &[f64], betas: &[f64]| -> Result<Mat<f64>, anyhow::Error> {
let steps = alphas.len();
if steps == 0 {
return Ok(Mat::zeros(0, 1));
}
// 1. Assemble T_k from coefficients using triplet format
let mut triplets = Vec::with_capacity(3 * steps - 2);
for (i, &alpha) in alphas.iter().enumerate() {
triplets.push(Triplet { row: i, col: i, val: alpha });
}
for (i, &beta) in betas.iter().enumerate() {
triplets.push(Triplet { row: i, col: i + 1, val: beta });
triplets.push(Triplet { row: i + 1, col: i, val: beta });
}
let t_k_sparse = SparseColMat::try_new_from_triplets(steps, steps, &triplets)?;
// 2. Construct e_1
let mut e1 = Mat::zeros(steps, 1);
e1.as_mut()[(0, 0)] = 1.0;
// 3. Solve T_k * y' = e_1 via sparse LU
Ok(t_k_sparse.as_ref().sp_lu()?.solve(e1.as_ref()))
};
The closure takes the coefficient arrays, constructs the sparse tridiagonal matrix, and solves the system. The triplet format lets us build the matrix efficiently without knowing its structure in advance. The sparse LU solver leverages the tridiagonal structure to avoid dense factorization.
Some interesting results
Now that we have a working implementation we can run some tests. The core idea of what we have done is simple: trade flops for better memory access. But does this trade actually pay off on real hardware? To find out, we need a reliable way to benchmark it.
For the data, we know that the performance of any Krylov method is tied to the operator’s spectral properties. We need a way to generate a family of test problems where we can precisely control the size, sparsity, and numerical difficulty. A great way to do this is with Karush-Kuhn-Tucker (KKT) systems, which are sparse, symmetric, and have a specific block structure.
A=(DETE0)A = \begin{pmatrix} D & E^T \ E & 0 \end{pmatrix}
This structure gives us two critical knobs to turn. First, with the netgen utility, we can control the EE matrix, which lets us dial in the problem dimension, nn. Second, we build the diagonal block D with random entries from a range [1,CD][1, C_D]. This parameter, CDC_D, gives us direct control over the numerical difficulty of the problem.
For a symmetric matrix like DD, the 2-norm condition number, κ2(D)\kappa_2(D), is the ratio of its largest to its smallest eigenvalue: κ2(D)=λmax(D)/λmin(D)\kappa_2(D) = \lambda_{\max}(D) / \lambda_{\min}(D). Since DD is diagonal, its eigenvalues are simply its diagonal entries. We are drawing these entries from a uniform distribution U[1,CD]U[1, C_D], so we have λmax(D)≈CD\lambda_{\max}(D) \approx C_D and λmin(D)≈1\lambda_{\min}(D) \approx 1. This means we get direct control, as κ2(D)≈CD\kappa_2(D) \approx C_D.The spectral properties of this block heavily influence the spectrum of the entire matrix AA. A large condition number in DD leads to a more ill-conditioned system for AA. The convergence rate of Krylov methods like Lanczos is fundamentally governed by the distribution of the operator’s eigenvalues. An ill-conditioned matrix, with a wide spread of eigenvalues, will require more iterations, kk, to reach the desired accuracy. By simply adjusting the CDC_D parameter, we can generate everything from well-conditioned problems that converge quickly to ill-conditioned ones that force us to run a large number of iterations. This is exactly what we need to rigorously test our implementation.
Memory and Computation Trade-off
We measure the algorithm against two hypotheses on a large sparse problem with n=500,000n=500,000, varying the number of iterations kk.
Hypothesis 1 (Memory): The one-pass method stores the full basis Vk\mathbf{V}_k with complexity O(nk)O(nk). We expect its memory to grow linearly with kk. The two-pass method operates with O(n)O(n) memory, so it should have a flat profile.
Hypothesis 2 (Runtime): The two-pass method performs 2k2k matrix-vector products instead of kk. If all else were equal, we’d expect it to run twice as slow.
Memory Usage
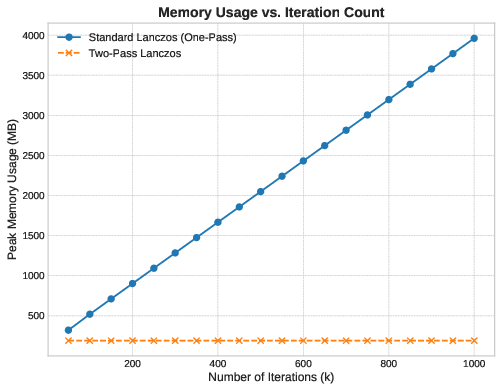
The memory data confirms Hypothesis 1 exactly. The one-pass method’s footprint scales as a straight line—each additional iteration adds one vector to the basis. The two-pass method remains flat. No allocation growth happens after initialization.
Runtime: Where Theory Breaks
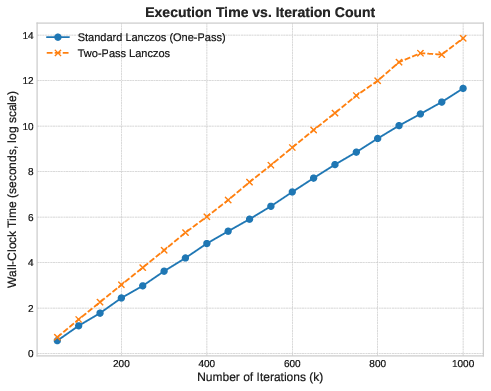
The runtime data contradicts Hypothesis 2. The two-pass method is slower, but never by a factor of two. For small kk, the gap is minimal. As kk grows, the two-pass runtime diverges slowly from the one-pass method, not by doubling, but by a much smaller margin.
This difference comes from memory access patterns. Both methods perform matrix-vector products, but they differ in how they reconstruct the solution.
The one-pass method computes xk=Vkyk\mathbf{x}_k = \mathbf{V}_k \mathbf{y}_k in a single dense matrix-vector product. When nn and kk are large, the n×kn \times k basis matrix exceeds all cache levels. The CPU cannot keep the data resident; instead, it streams Vk\mathbf{V}_k from main memory. This is a memory-bandwidth-bound operation. The processor stalls, waiting for each load to complete. Instruction-level parallelism collapses.
The two-pass method reconstructs the solution incrementally. At each iteration, it operates on exactly three n-dimensional vectors: vprev\mathbf{v}_{\text{prev}}, vcurr\mathbf{v}_{\text{curr}}, and xk\mathbf{x}_k. This working set fits in L1 cache. The processor performs 2k2k matrix-vector products (each one reading the sparse operator, then applying it to a cached vector), but the solution accumulation happens entirely within cache. The additional matrix-vector products are cheaper than the memory latency of the standard method.
The cost of re-computing basis vectors is less than the latency cost of scanning an n×kn \times k dense matrix from main memory.
Medium-Scale Behavior
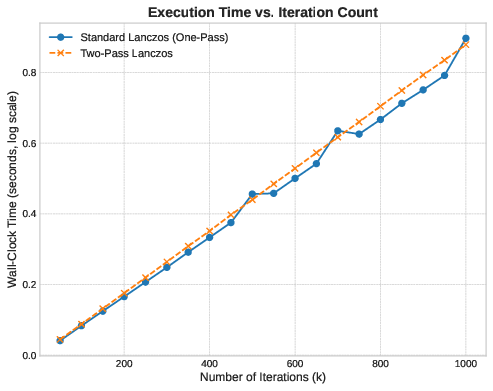
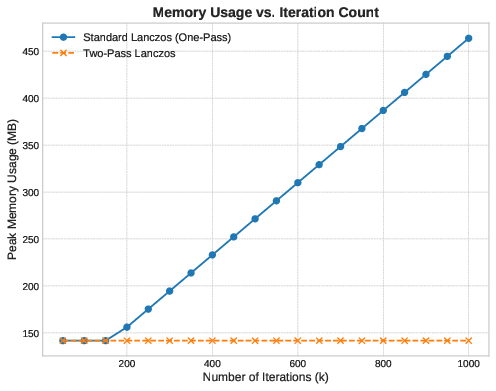
At n=50,000n=50,000 we can observe an equilibrium. The two methods have nearly identical runtime. The standard method’s Vk\mathbf{V}_k matrix is smaller; it fits partially in cache. The cache-miss penalty here becomes manageable. The two-pass method still has the advantage of cache-local accumulation, but the difference is marginal.
What About Dense Matrices?
To be sure of our hypothesis, we can test it directly using a dense matrix of size n=10,000n=10,000. For dense problems, the matrix-vector product is O(n2)O(n^2), it dominates all other costs. Memory latency will become negligible relative to the compute work and the cache efficiency advantage should disappear.
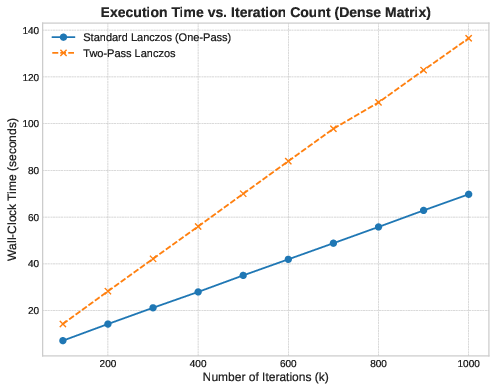
We can see that the two-pass method runs almost exactly twice as slow as the one-pass method. The slope ratio is exactly 2:1. In a compute-bound regime, the extra matrix-vector products cannot be hidden by cache effects. Here, the theoretical trade-off holds perfectly.
Scalability
Now, let’s fix the iteration count at k=500k=500 and vary nn from 50,00050,000 to 500,000500,000 to measure scalability. Based on what we have seen before, we would expect the two-pass memory to scale linearly with nn but with a small constant factor (three vectors, plus scalars). The one-pass method should also scale linearly, but with a kk-dependent slope.
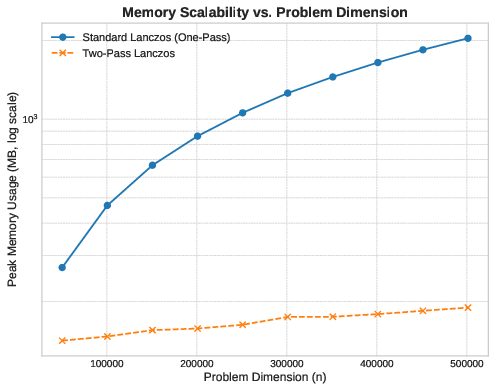
Here we have to use a logarithmic y-axis to show both curves; the two-pass line is so flat relative to the one-pass line that it’s otherwise invisible.
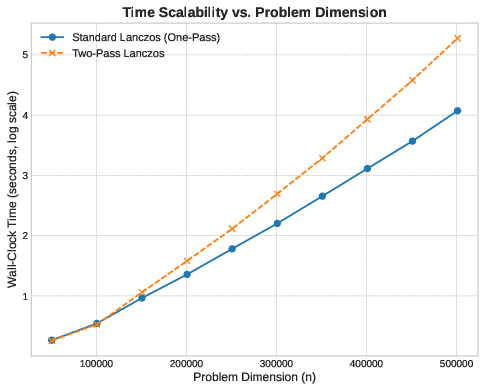
Runtime scales linearly with nn for both methods, as expected. Below n=150,000n=150,000, the two methods have similar performance. This is the regime where both basis and working set fit in cache, or where the problem is small enough that memory latency is not the bottleneck.
As nn increases beyond 150,000150,000, the matrix-vector product time dominates. The sparse structure of A\mathbf{A} ensures that each matvec requires multiple memory accesses per element. For the one-pass method, the final reconstruction of Vkyk\mathbf{V}_k \mathbf{y}_k begins to cost more as the matrix grows. For the two-pass method, performing 2k2k matrix-vector products means the matvec cost accumulates more rapidly. The divergence is gradual, not sharp, because the advantage of cache locality in accumulation persists—but it cannot overcome the fundamental cost of doubling the number of expensive operations.
Well, that’s it. If you want to have a better look at the code or use it, it’s all open source:
This was more of an exploration than a production-ready library, so expect rough edges. But I hope it gives an interesting perspective on how algorithm engineering and low-level implementation details can alter what seems like a straightforward trade-off on a blackboard.