In this article, you will learn how GPT-5 handles intermediate to advanced mathematical reasoning, including solving systems of equations and constructing clean, textbook-style proofs.

Topics we will cover include:

• A quick, methodical warmup on solving a 2×2 linear system.
• Proofs about monotonicity and function ranges, written clearly and rigorously.
• Discussion of response quality, tone, and where the model still feels mechanical. Let’s get right to it.

Is ChatGPT-5 Able to Provide Proofs for Advanced Mathematics? Image by Editor

Introduction

One of the claims made by OpenAI regarding its latest model, GPT-5, is a breakthrough in reasoning for math and logic, with the ability to “think” more deeply when a prompt benefits from careful analysis. This includes complex, human-like reasoning settings such as coding, science questions, synthesizing information, or analyzing financial data. In mathematics, the model reportedly achieved a 94.6% success rate on math problem solving at the AIME 2025 international conference, without relying on external tools, demonstrating significant improvements over previous versions.

This article showcases — through examples of intermediate to advanced mathematical reasoning — how the latest version of ChatGPT tackles complex mathematical problems with strong accuracy and a notably methodical analytical approach. We also provide a brief discussion about the behavior exhibited in the responses obtained.

Disclaimer: while the intention here is not to go as far as shown in this Reddit post that claims ChatGPT-5 innovated by creating “new math,” we will briefly analyze the model’s capabilities to build elaborate, solid proofs for a variety of problems.

Warmup: Solving a System of Linear Equations

We will start with something gentle and purely methodological before moving to a more challenging problem: solving a system of two linear equations with two variables, x and y.

The system is as follows (taken from these lecture notes):

12	5x−2y=7−2x+y=3

And the prompt is simple, leaving the model free to choose its reasoning approach:

Solve the following system of linear equations: (followed by the above system as such)

This is the response ChatGPT returns:

Image by Author

Not only did the model solve the system correctly, with x = 13 and y = 29 as the true solution—it also showed a clear step-by-step method (e.g. substitution or elimination) and kept the algebra tidy.

Interestingly, if we also ask ChatGPT to choose the most efficient method from the available ones to solve the system—and to justify the choice — it might (and did, in my case) produce two possible answers and let you pick your preferred one.

Image by Author

Both answers resort to the same method — elimination — which shows how ChatGPT remains prompt-oriented and logically consistent rather than “creative” for its own sake (for example, by intentionally producing two different methods). The step-by-step reasoning is also similar in both cases, with the main difference being the style used to justify elimination.

A Bit More Challenge: Examples of Mathematical Proofs

Moving into more advanced, university-level math, we asked ChatGPT to construct proofs without providing specific example functions:

Prove that the composition of any two decreasing functions is increasing.

Without explicitly activating one of ChatGPT’s newest modalities, called the think longer mode, the app provided a convincing response that reads like a self-contained proof.

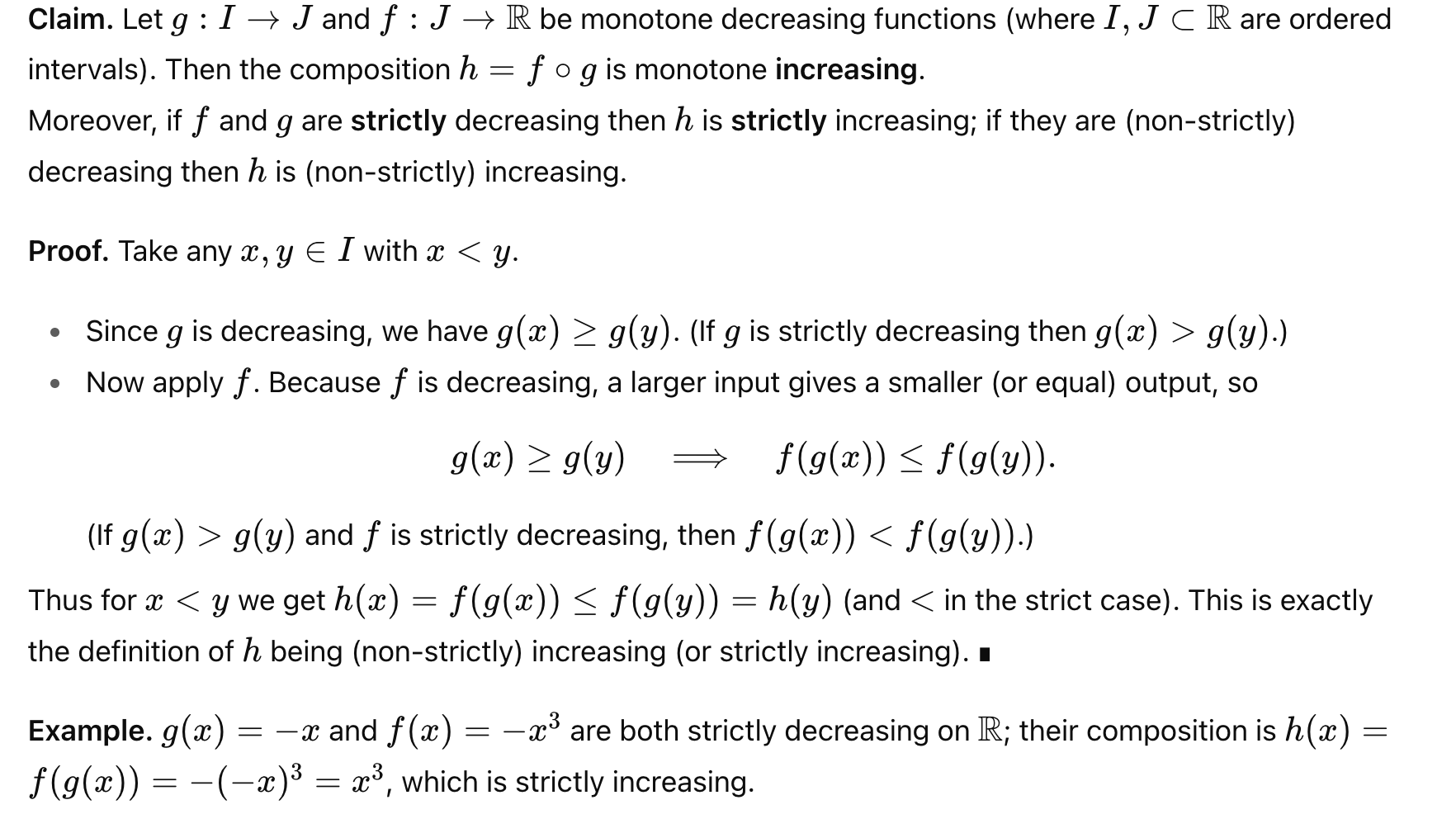
Image by Author

It can be easily verified—via solutions available on the Web, such as this example—that GPT-5 handled this challenge cleanly.

Here’s another example.

Let g(x) = 2x + 3x for |x| ≤ 1. (So the domain of g is [−1, 1].) Prove that the range of g is exactly [5/6, 5].

Image by Author

And the proof is, indeed, annoyingly correct! There’s nothing wrong with it, and there’s little to nitpick. Overall, the proof structure is complete and flows logically. Further, it correctly identifies the key properties of g(x): monotonicity, continuity, and differentiability. If we wanted to be picky, the narrative remains somewhat mechanical and low-engagement (e.g. it could include friendly signposts such as “here comes the tricky part” or “the next step is easy to digest”). To be fair, though, a formal, neutral tone is often appropriate for presenting a proof. Beyond tone, there’s little to question from a mathematical standpoint.

Wrapping Up

This article illustrated intermediate to advanced mathematical reasoning and problem-solving by OpenAI’s newest model, GPT-5. Through a few examples, the model’s accuracy and methodical depth were on display, followed by brief reflections on its results and the approach used to generate them.

No comments yet.

Leave a Reply