In a previous article, I introduced a new measure of disorder that I called (Amp), and attempted to determine whether it was a measure of presortedness. While trying to formally prove each of the 5 axioms required for a measure of presortedness, I discovered a counterexample showing that my measure did not satisfy the 4th axiom:

If every element of a sequence (X) is smaller than every element of another sequence (Y), then (M(XY) \le M(X) + M(Y))

A counterexample can be constructed as follows: (Amp) considers a single descending run to be sorted, but two descending runs, the second greater than the first, not sorted:

• ‎(Amp(\langle 4, 3, 2, 1, 0 \rangle) = 0)
• ‎(Amp(\langle 9, 8, 7, 6, 5 \rangle) = 0)
• ‎(Amp(\langle 4, 3, 2, 1, 0, 9, 8, 7, 6, 5 \rangle) = 2)

This simple counterexample, besides crushing my hopes and dreams, made me question how much order there can be in a descending run. Which by itself is a bit of a philosophical quest for meaning.

Intuitive disorder of a descending run

[X = \langle 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 \rangle]

Intuitively, a strictly descending run like (X) above is already extremely ordered, albeit in a “descending” order instead of an “ascending” one:

• If we can visit the elements of the sequence backwards, it is just as ordered as an ascending run.
• Using (>) as a predicate for ordering instead of (<) tells us that there’s no disorder in that sequence.

If our goal however is to reorder the elements so that they end up in ascending order—that is, if we decide to look at the problem through the lens of work instead of information—then the answer is different:

• It requires a single reversal of the sequence.
• Though such a reversal corresponds to (\frac{\lvert X \rvert}{2}) element swaps.
• If we are dealing with a doubly linked list, we can swap (\lvert X \rvert) pointers instead of swapping elements.
• Or we can insert (\lvert X \rvert) times the last element of the collection at the beginning.

Interestingly, the disorder feels constant when looking at the problem strictly from an ordering point of view, but becomes linear when looking at it through the lens of work needed to reorder the sequence.

Through the prism of measures of disorder

As an experiment, I decided to give the sequence above to all measures of disorder I understand to see what they had to say. For readability purposes, I split them in two groups below, based on their answer. The number between parenthesis corresponds to the theoretical maximum of the measure for a sequence of that size.

Note: all measures of disorder below are given in their “purest” form, that is, not tweaked to give 0 when a sequence is already ordered.

(X) has high disorder:

• (Block(X) = 10 : (10)), the number of elements in (X) that are not followed by the same element in the sorted permutation.
• (Dis(X) = 9 : (9)), the maximum distance determined by an inversion.
• (Exc(X) = 5 : (10)), the minimum number of exchanges required to sort (X).
• (Ham(X) = 10 : (10)), the number of elements in (X) that are not in their sorted position.
• (Inv(X) = 45 : (45)), the number of inversions in (X).
• (Max(X) = 9 : (9)), the maximum distance an element in (X) must travel to find its sorted position.
• (Rem(X) = 9 : (9)), the minimum number of elements that must be removed from (X) to obtain a sorted subsequence.
• (Runs(X) = 10 : (10)), the number of increasing runs in (X).
• (Spear(X) = 50 : (50)), the sum of distances between the position of individual elements in (X) and their position in its sorted permutation.
• (SUS(X) = 10 : (10)), the minimum number of increasing subsequences (of possibly non-adjacent elements) into which (X) can be decomposed.

A first observation here is that we find all measures of disorder based on the sorted position of the elements ((Block), (Dis)?, (Exc), (Ham), (Max) and (Spear)), as well as those that look for exclusively ascending sequences of some sort ((Rem), (Runs) and (SUS)).

(X) has low disorder:

• (Amp(X) = 0 : (8)), the amplitude of the prefix sum of pairwise difference (see here).
• (Enc(X) = 1 : (5)), the number of encroaching lists that can be extracted from (X).
• (Mono(X) = 1 : (5)), the number of increasing and decreasing runs in (X).
• (Osc(X) = 0 : (40)), the oscillation of (X)1.
• (SMS(X) = 1 : (4)), the minimum number of increasing or decreasing subsequences (of possibly non-adjacent elements) into which (X) can be decomposed.

Here we have two main subcategories of measures: those that explicitly look for ascending and descending sequences ((Enc), (Mono) and (SMS)), and those where the result naturally arises from a symmetry between a sequence, and a similar sequence in reversed order ((Amp) and (Osc)).

A second observation is that none of those measures respect Mannila’s axioms:

• (Enc), (Mono) and (SMS) return (1) for a sorted sequence, when axiom 1 expects them to return (0).
• (Amp) and (Osc) both violate axiom 4 with the example given in the article introduction.

Symmetry and measures of presortedness: pick one

It might seem odd at first that none of the measures of disorder that return (0) or (1) for a descending run qualifies as a measure of presortedness, though an explanation might be found in the symmetry property. Indeed the five measures of interest return the same result both for an ascending run and a descending run, and all but (Exc) are actually perfectly symmetric over the input sequence23: accepting any sequence forward or backward returns the same result.

In fact, we can already see an incompatibility: if any measure of disorder that returns (0) both for an ascending run and for a descending run, then it also has to return (0) for the counterexample in the article introduction, failing which it does not respect Mannila’s 4th axiom. Going further, such a measure of disorder would have to return (0) for any sequence that’s made of any combination of ascending and descending runs of any size as long as all elements of one of those are greater than the elements of all previous runs4, such as in the following sequence:

The only measure of presortedness in the literature that provably implements this behavior is (m_0), a measure that returns (0) for all inputs. I am unsure whether it is feasible to come up with a different measure of presortedness that is both perfectly symmetric over its input, but also useful.

Note: this last example is fairly cute because we are back into a territory where some measures find very little disorder, for different reasons: (Dis) and (Max) return (1) because the inversion distance is minimal, and (SUS) finds (2) because the sequence can easily be decomposed into two increasing subsequences.

Can we adapt our reverse champions?

Among the measures discussed in the previous section, (Enc), (Mono) and (SMS) return (1) when given a single ascending run, which violates Mannila’s first axiom of what makes a measure of presortedness. It would be tempting to define derived measures that simply retrieve (1) from their result, the same way (Runs) is fixed by returning the number of runs minus (1) (or is redefined as returning the number of “step-down” in the sequence). However those three measures also return (1) for a descending run, so retrieving (1) would make them return (0) for a descending run, a result which would make them break the 4th axiom, as we discussed in the previous section.

In Sorting and Measures of Disorder, Vladimir Estivill-Castro recognizes the issue of (Enc) returning (1) for an ascending run, as well as the shortcomings of trying to use (Enc(X) - 1) to circumvent the issue. Instead he proposes a new equivalent measure based on (Enc), dubbed (M_{Enc}), which satisfies all five of Mannila’s axioms and is thus a proper measure of presortedness:

[M_{Enc}(X)= \begin{cases} 0 & \text{if } X \text{ is sorted,}\ Enc(X_{tail}) & \text{otherwise, where } X_{tail} \text{ is } X \text{ without its leading ascending run.} \end{cases}]

His technique of greedily singling out the first ascending run of the sequence allows to create just enough asymmetry to avoid the pitfall we described earlier. As an experiment, I tried to apply the same technique on the other four measures that exhibit low disorder for a single descending run, in a bid to turn more measures of disorder into measures of presortedness:

• (M_{Amp}) does not satisfy axiom 4: (M_{Amp}(\langle 2, 1, 0 \rangle) = 1), (M_{Amp}(\langle 4, 3 \rangle) = 1), but (M_{Amp}(\langle 2, 1, 0, 4, 3 \rangle) = 3).
• (M_{Mono}) does not satisfy axiom 4: (M_{Mono}(\langle 1, 0 \rangle) = 1), (M_{Mono}(\langle 2, 3 \rangle) = 0), but (M_{Mono}(\langle 1, 0, 2, 3 \rangle) = 2).
• (M_{Osc}) does not satisfy axiom 4: (M_{Osc}(\langle 1, 0 \rangle) = 0), (M_{Osc}(\langle 3, 2 \rangle) = 0), but (M_{Osc}(\langle 1, 0, 3, 2 \rangle) = 1).
• Computing (SMS) is an NP-complete problem5, so I can’t reasonably experiment with (M_{SMS}).

Welp, I guess it was worth a try. At least those counterexamples save me from having to prove anything formally this time.

Conclusion

I am unsure where exactly I wanted to go when I first started writing this blog post. In the end we only end up with a few weak conclusions:

• Whether a descending run contains disorder or not depends on how we look at the problem, and on what we want to do with said sequence.
• If a measure of disorder finds (0) for a descending run, it is unlikely to be a measure of presortedness.
• If a measure of disorder is perfectly symmetrical over the input sequence, it is unlikely to be a measure of presortedness.
• None of the existing measures of disorder that consider a descending run ordered are measures of presortedness in their purest form.
• It might be possible to adapt such measures of disorder to become measures of presortedness, but I don’t know any generic method.

I hope that I can revisit some aspects touched by this article in the future, and come up with stronger conclusions. In the meantime, I do find amusing that trying to answer a question once again opens a few doors towards other questions.

Notes

(Osc(X)) is formally defined as (\sum_{i=0}^{\lvert X \rvert - 1} \vert \vert Cross(x_i) \vert \vert) where (Cross(x_i)) corresponds to the number links between adjacent pairs that “cross” the value (x_i). In the following image, (Cross(x_5) = { 1, 3, 6 }), and (Osc(X) = 17): 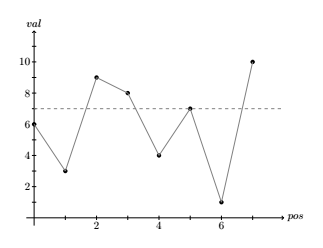↩ 1.

(Enc(\langle 4, 5, 3, 6, 2, 7, 1, 8, 0, 9 \rangle) = 1), but (Enc) returns (5) (its maximum) over the same sequence reversed. ↩ 1.

The symmetry of (Osc) is mentioned in Adaptive Heapsort by C. Levcopoulos and O. Petersson, the symmtry of (Amp) is proven in my previous article Symmetry of Amp, the symmetry of (Mono) and (SMS) are only conjectured as far as I know but arise intuitively from their definition. ↩ 1.

Computing how many such sequences exist for a given size is left as an exercise to the reader. ↩ 1.

See Sorting Shuffled Monotone Sequences by C. Levcopoulos and O. Petersson. ↩