Introduction

In this inquiry, nodes are connected one at a time. How many lines can you draw before a triangle emerges?

Starting with Four

Let’s start with four nodes - draw them on a sheet of paper. How many lines (called edges) can you draw before a triangle forms with each vertex on a node? (Don’t count triangles that don’t have vertices on a node).

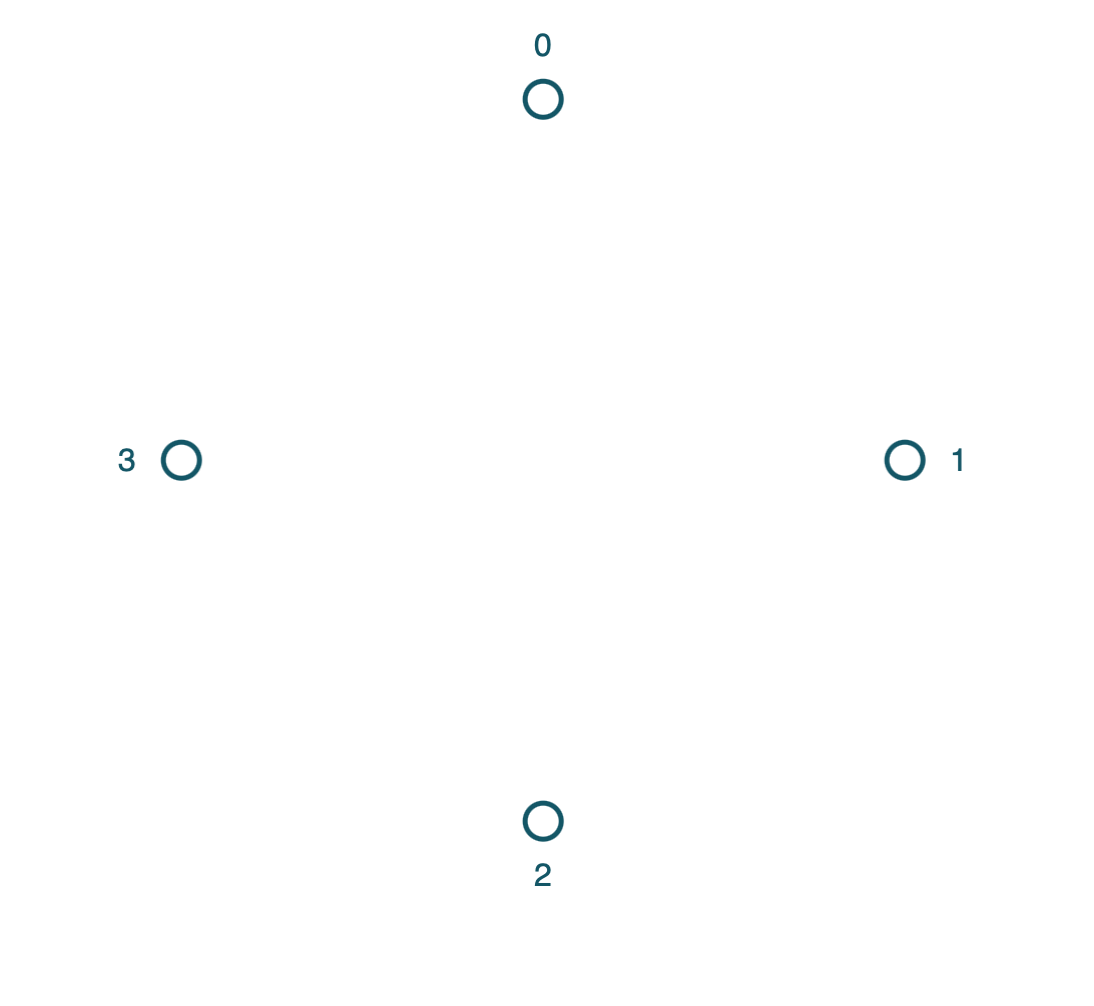
What is the fewest number of edges you can draw before there has to be a triangle? What is the largest number of edges you can draw before there has to be a triangle?

More Numbers

Now, play with graphs that have 6, 8, and 10 nodes. There is a tool below. You can either start with all lines and remove some of them, or add lines. Paper works as well.

Graphing tool to connect nodes equidistant from the center. When a triangle forms with all vertices on nodes, it shades it in with orange.

Activity

• Play with adding edges in different ways. Look at even and odd numbers of nodes. Examine symmetrical and randomly generated graphs.
• Is there a strategy to maximize or minimize the number of edges you can fit without any triangles emerging?
• What patterns do you notice? What conjectures can you form from your observations and play?
• What other questions can you pose?

Activity Structure

This is a 60+ minute activity.

Exploration Phase (15-30 minutes)

Playing with a 6-node graph

Explore a 6-node graph and see what the maximum number of lines is possible without any triangles. Some of the ways learners may approach this:

• Whiteboard group work (virtual or in person)
• Using the interactive tool and taking screenshots to share
• Paper and pencil
• No graph - how could you restate the problem and work it without a graph?
• Build a spreadsheet of observations.

If learners find 9 lines are possible, then try a 4-node graph to note that 4 lines are possible.

Then try 8 nodes.

• Some may get 12 for an 8-node graph, but more are possible. Here are some questions to help:

• How do you know that this way of drawing maximizes the number of lines possible?

• What is the smallest number of lines for each graph we’ve looked at? This might tell us how not to draw it.

• If two nodes are connected, what can we say about what other nodes they can connect to? (They can’t both connect to the same node.)

• Splitting the graph into two colors and connecting with different rules that way (only red to blue, or blue to blue, or ...). Be cautious with this nudge - it may reveal too much. Even and odd-numbered nodes also work for this.

Conjecture Formation (15-30 minutes)

Allow time to write down observations and form conjectures using the even node graphs as a starting point. Give examples of conjectures, if needed, that don’t give away discoveries.

The table below shows just how many patterns may emerge from adding, subtracting, and playing with the different columns (It’s fun to discover, so the table is just for reference as a facilitator)

Nodes	Possible Edges	Possible Triangles	Max lines no Triangle
3	3	1	2
4	6	4	4
5	10	10	6
6	15	20	9
7	21	35	12
8	28	56	16
9	36	84	20
10	45	120	25
11	55	165	30

Possible Conjectures (these are just a few):

“The number of maximum lines for an even number of nodes is (n/2)(n/2).”

“The number of maximum lines for an odd number of nodes is (n+1)(n-1)/4.”

The number of maximum lines to not form a triangle is the number of possible lines minus the (n-1) graph’s maximum number of lines to not form a triangle.

“Starting with a 3-node graph, the maximum number of lines that don’t form a triangle is {2,4,6,9,12,16,20,...}, where there is adding in the pattern {+2,+2,+3,+3,+4,+4,...}.”

“For even node graphs, the maximum number of lines is a square number.”

“The worst way to draw a graph is to connect all of the nodes to a single node.”

“The best way to draw a graph is to connect all even nodes to odd nodes, and not even to even or odd to odd.”

Other conjectures related to colorings, such as what makes a cycle of 4, and more, can emerge - go with the flow to see what is discovered.

Discussion (10-20 minutes)

Share and discuss conjectures, observations, and strategies.

What patterns emerged? What other strategies or approaches were taken?

Create a table or document to record observations in various ways.

Look at all the graphs created! Do any insights emerge when seeing other peoples approaches?

Optional Extensions - try a proof or variation

Numerous conjectures and observations can arise from this activity; only one proof outline is below. Learners may also find that spending more time in the pattern-finding space suits them well for this activity. Instead of proofs, variations and games can be played with the graphs (don’t make 4, nim-like turns of drawing lines (Sim), colorings, and more).

One approach is to split the nodes into two groups and make a bipartite graph, where each group can connect to the other, but not to itself.

Proof-1: A graph with even nodes can have a maximum of (n² - 1)/4 edges without forming any triangles.

1. A triangle forms when two connected nodes both connect to a third node.
2. To avoid triangles, split all nodes into two groups (A and B) and only connect nodes between groups, never within a group.

• This prevents triangles because any two connected nodes are in different groups, so that no third node can connect to both.

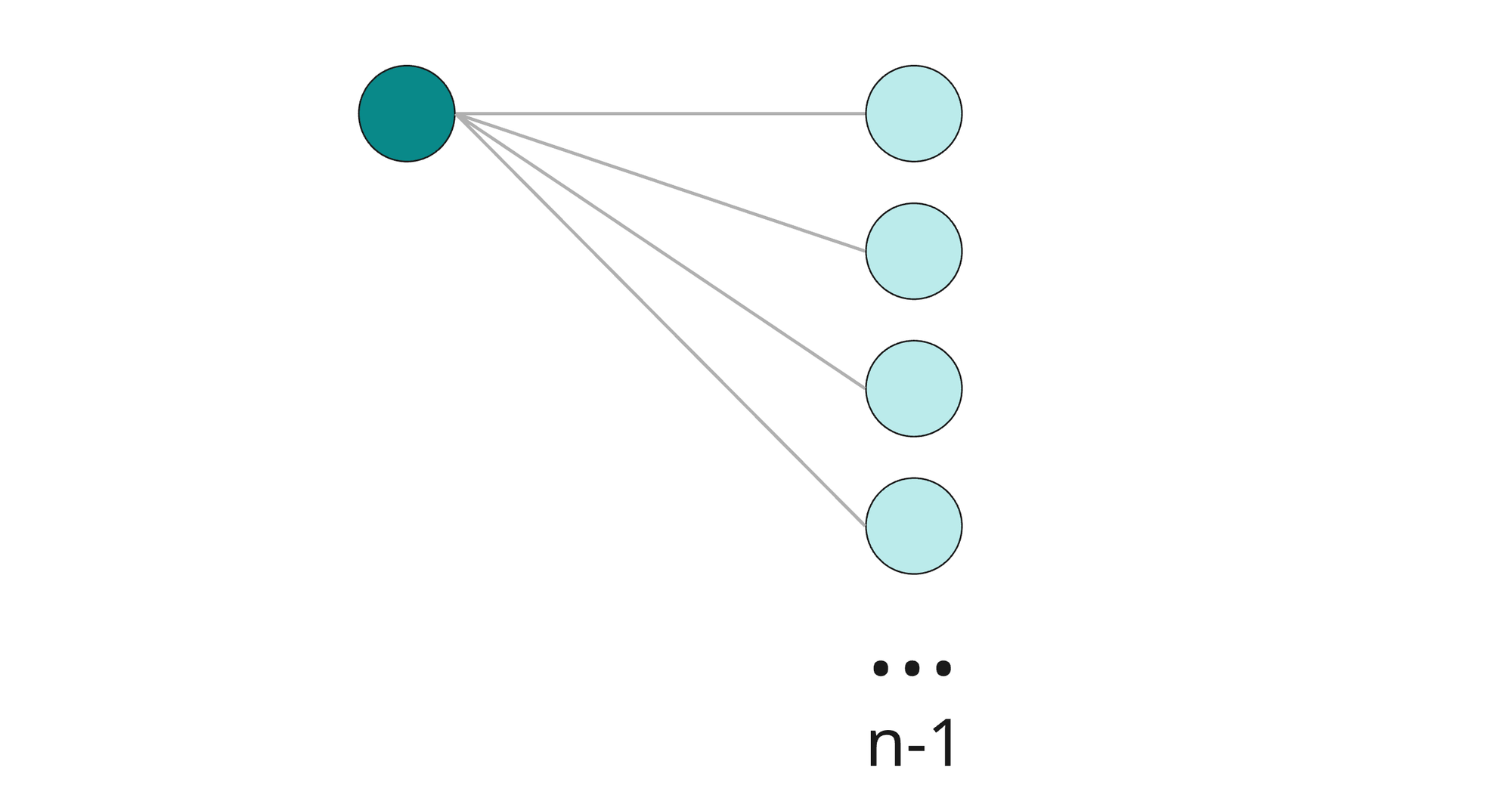
1. If Group A has k nodes and Group B has (n - k) nodes, the number of edges is k(n - k).

• Or said another way: An edge connects exactly one node from Group A to exactly one node from Group B, so counting all possible pairs gives k(n - k) edges.

1. When k = 1, there are n - 1 edges. This is the lower bound.

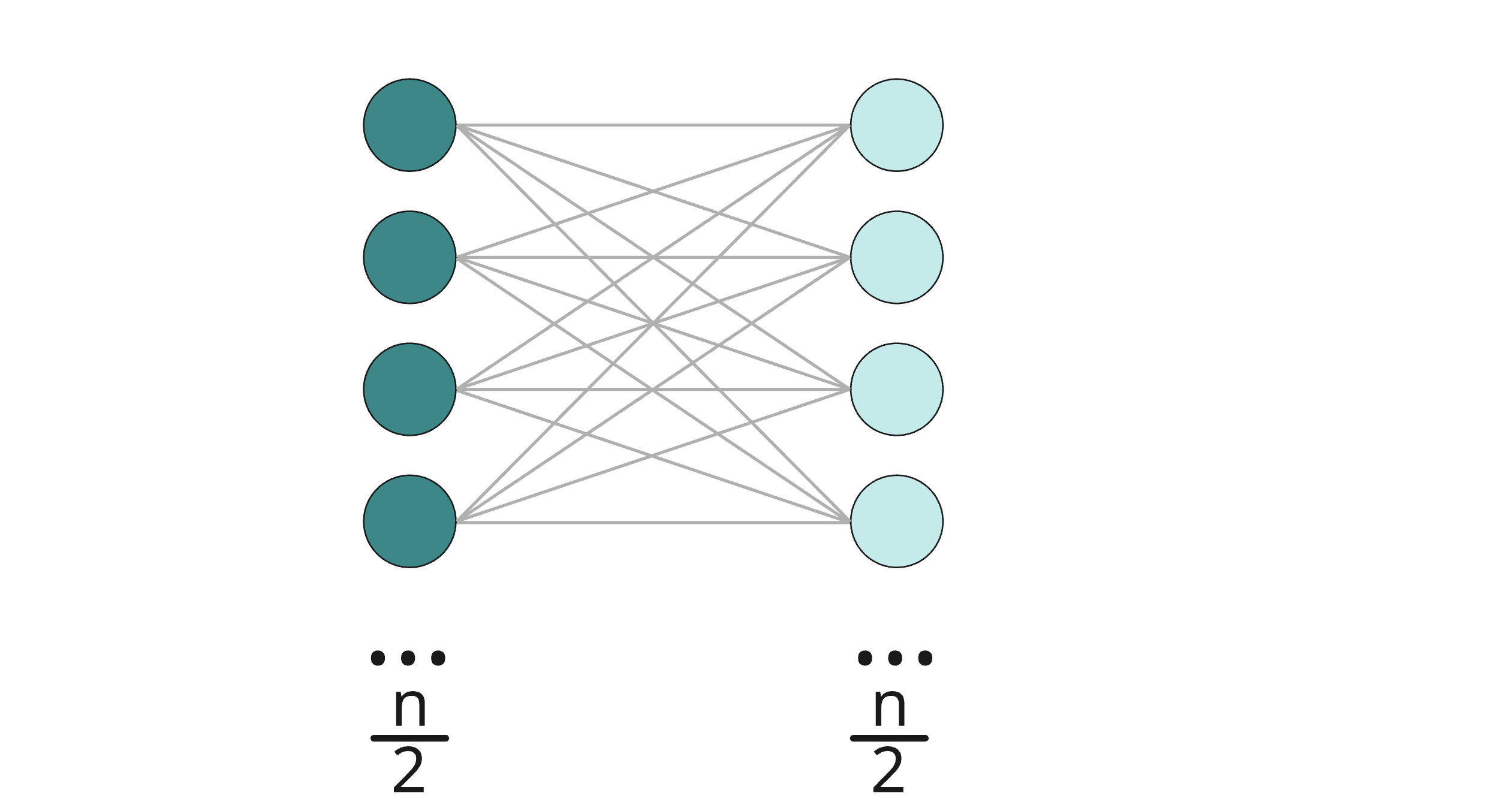
2. When k = n/2, we get (n/2)(n/2) = n²/4 edges. This is the upper bound, since anything larger than n/2 is the same as a smaller value of k.

3. The maximum occurs when the groups are equal in size – when k = n/2, resulting in n²/4 edges in this two-group graph, also known as a bipartite graph.

4. The maximum number of edges without triangles is n²/4.

Proof-2: The maximum number of lines for an odd graph that can exist without forming a triangle is (n² - 1)/4.

Steps 1-4 of Proof-1.

1. When n is odd, we cannot split evenly. The closest split is k = (n+1)/2 and (n - k) = (n-1)/2. This is the upper bound, because anything larger is the same as a smaller value of k.
2. This gives ((n+1)/2)((n-1)/2) = (n² - 1)/4 edges.
3. Therefore, the maximum number of edges without triangles when n is odd is ((n+1)/2)((n-1)/2) = (n² - 1)/4.

Tools and Supplies

• Paper, pencils, or a whiteboard.

Vocabulary

• Node: A point in a graph that can be connected to other nodes by edges.
• Edge: A connection between two nodes in a graph.
• Triangle: A cycle of three nodes where each node connects to the other two, forming a closed loop.
• Bipartite Graph: A graph where nodes are split into two groups, and edges only connect nodes from different groups—no nodes within the same group are connected.
• Graph: A collection of nodes and the edges that connect them.
• Partition: Splitting a set of nodes into separate groups.
• Maximum: The largest possible value that can be achieved under given constraints.
• Parity: Whether a number is odd or even.
• Proof: A logical argument that demonstrates why a mathematical statement must be true.

Resources, Extensions, and What Ifs

• What about avoiding other cycles (of 4 or 5) instead of triangles? How many edges can you have if you can’t form any 4-cycles?
• **Mantel’s Theorem **
• Turán’s Theorem
• Splitting into three or more groups
• Directional graphs
• Real-world: when do we want to avoid triangles?
• Ramsey numbers