The University of Tokyo has made itself one of the most important research centers in the world for quantum algorithm design, and helped make Japan into a global quantum computing leader.

Right now, much of the most urgent work happening in quantum computing is in algorithm design. Publicly-available IBM quantum computers are already executing workloads that test the limits of what’s possible on classical supercomputers, and the hardware improves every year. However, the key to quantum advantage—where a quantum computer can run a computation more accurately, cheaply, or efficiently than a classical computer alone—is developing powerful algorithms that maximize the capabilities of existing quantum computers.

Some key efforts toward this goal have come from the University of Tokyo. UTokyo associate professor Nobuyuki Yoshioka, IBM Principal Research Scientist Antonio Mezzacapo and their collaborators developed an algorithm for “Krylov quantum diagonalization” (KQD) that has become a cornerstone of some of the most promising research now happening in quantum computing.

KQD, which the researchers described in a paper published in June 2025 in Nature Communications, is at its core a technique for finding the ground state of a system. The ground state is the lowest-energy state where the system rests if nothing perturbs it. In a classical physics example, the ground state of a bowling ball in a half-pipe is sitting still at the bottom between the two slopes. If you see it moving around or balancing on the lip of the half-pipe, that’s an excited state.

In practice, calculating the ground state of physical systems—particularly when there are many bodies involved interacting with quantum effects—is often challenging even for powerful supercomputers. For example, what is the ground state of an organic molecule composed of hundreds of mutually-interacting particles in a chain? That value can give scientists important information about how those systems really behave.

Today, classical supercomputers spend a great deal of their time working on these sorts of problems. Better methods for calculating the ground states of many-body systems could open new pathways to research in fields ranging from chemistry to high-energy physics.

KQD is part of a string of recent results of quantum algorithm development efforts that seek to calculate the ground states of complex systems better than classical methods alone. Others include sample-based quantum diagonalization and sample-based Krylov quantum diagonalization. The work by Yoshioka and his collaborators’ has already fed forward into sample-based Krylov quantum diagonalization (SKQD) which is one of the most promising avenues for quantum advantage and industrial application.

Why algorithms like KQD are important

It’s algorithms that make quantum computers useful. When Paul Benioff described the first quantum mechanical model of a computer in a 1980 paper, it didn’t mention chips or hardware. Peter Shor did not consider the practical limits of qubits when he published his famous quantum algorithm for factoring in 1994, nor did Lov Grover when he published his algorithm in 1996.

However, it’s these algorithms that kicked off the subsequent decades of hardware development that resulted in today’s utility-scale quantum computers. And now, the technology is at a stage where it can be useful for real-world work beyond classical computing alone—though not yet at the scale to run meaningfully large instantiations of Grover’s, Shor’s, or other algorithms. Therefore, quantum needs well-designed algorithms to realize its potential today.

Quantum computers have matured enough to begin solving problems beyond the capabilities of classical computers, but they remain in an early stage of development comparable to classical computers in the mid-20th century. Researchers are still figuring out the full extent of problems they can solve, and developing algorithms to make best use of existing hardware and the hardware we expect to deliver in the near future.

Fault-tolerant quantum computers capable of returning accurate values for long quantum circuits are on their way. IBM plans to deliver IBM Quantum Starling, the first such computer, by 2029. Today’s 100+ qubit quantum computers are already advanced enough that they can deliver valuable results. Today’s task is realizing that value through clever algorithm design.

The work researchers do today to develop great algorithms will extend and scale as Starling (and eventually IBM Quantum Blue Jay) make it possible to do bigger, deeper executions.

“Especially at this stage of the technology, before we reach thousands of error-corrected qubits, algorithms that allow us to solve challenging computational problems with the current level of computational resources are very useful,” said Hanhee Paik, Director of Quantum Algorithms Centers at IBM Research.

Understanding KQD

KQD at its core is a method for using a quantum computer to solve a linear algebra problem.

Linear algebra is the mathematics of linear equations, which simplifies solving into manipulating vectors using matrices—numbers arranged in rows and columns. Diagonalizing matrices transforms them such that the most important numbers in the array are arranged along the diagonal from the upper left to the bottom right. This is, in a sense, a simplified representation of the information from the original matrix that is easier to work with mathematically.

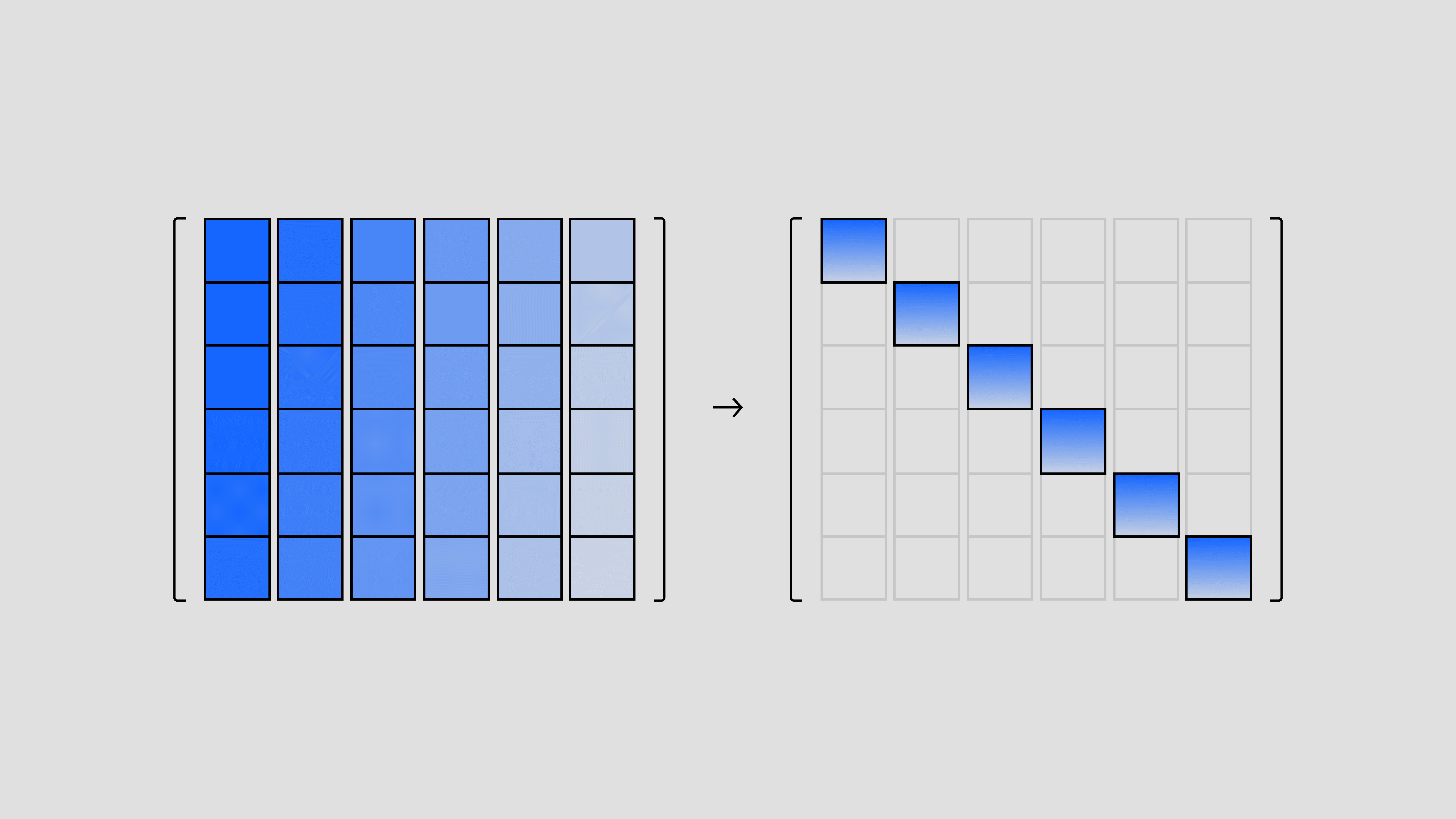
When a matrix represents a physical system in the real world, diagonalizing that matrix means finding the ground state of the system.

“We use diagonalization to compute the energy landscape of a wide range of physical systems,” Yoshioka said. “Not only in physics, but also in chemistry, mathematics, and even machine learning. We always want to use this diagonalization to investigate the important qualities of the quantum system.”

Until a few years ago, the go-to quantum method for finding the ground state of a system was a heuristic approach called the variational quantum eigensolver (VQE). However, VQE is difficult to scale, and does not always successfully deliver a solution to a problem.

Researchers kept looking for good quantum methods for solving linear algebra problems, with good reason: Diagonalization can be extremely difficult for very complex, multi-dimensional problems—the sort that come up when simulating complex many-body physical systems like large molecules in chemistry—but the results can be valuable.

In 1931, Russian engineer and mathematician Aleksey Krylov developed a technique that makes this faster and easier by cleverly constructing subspaces—parts of the matrix—that capture its important features. Using these Krylov subspaces, and making a few modest assumptions about the matrix, enables a calculation that converges to the correct result.

Yoshioka and Mezzacapo looked at the Krylov method for a potentially more efficient, exact alternative that will always “converge” on a solution. In their approach, the mechanics of the quantum computer take on the computational load of the most classically difficult parts of performing Krylov diagonalization: generating the Krylov subspaces. It turns out that the time-evolution of qubits involves analogous operations to those used to classically generate Krylov subspaces. As the qubits—which are set up to represent mathematical operators from Krylov subspaces—evolve over time, they help solve the problem exactly. Combined with advanced error mitigation techniques, KQD could deliver far better, more precise results than VQE.

At the same time as Yoshioka, Mezzacapo, and their colleagues were developing KQD, other teams of researchers developed a different approach to solving linear algebra problems on quantum computers called sample-based quantum diagonalization (SQD). KQD tends to be best for condensed matter problems, and SQD for chemistry problems. Both methods have led to dramatic improvements in the ability of quantum computers to find the ground states of complex systems.

Researchers combined KQD and SQD to create SKQD. In SKQD, the problem is broken up into Krylov subspaces, then those subspaces are sampled to quickly find solutions. This is one of the most promising avenues for quantum advantage in the near term.

How the University of Tokyo made itself a quantum leader

In 2020, IBM and the University of Tokyo partnered to advance quantum computing in Japan. In 2021, IBM installed an IBM Quantum System One in Kawasaki City.

IBM Quantum System One at University of Tokyo.

The University of Tokyo is home to many of the world’s most creative researchers. And they have made the best of the opportunity created through the IBM quantum partnership. As of this writing, Tokyo researchers have produced 64 quantum papers in collaboration with IBM, a remarkable rate of output in just a short period of time.

Koji Terashi, University of Tokyo physics professor, head of the IBM-UTokyo lab, and special advisor to the university president on quantum computing, said that the collaboration has driven interest in quantum computing both within and beyond the university itself.

This is the result of the early and strong commitment the University of Tokyo and Japanese government made in quantum computing, supported by a strong societal interest in the technology.

“This success is driven by the unique strengths each side brings to the collaboration. The University of Tokyo offers deep theoretical insight and a vibrant academic environment, while IBM provides access to advanced quantum hardware, software, and a global network of quantum expertise. Together, they’ve created a dynamic ecosystem where fundamental research and practical innovation reinforce each other,” said Hiroshi Horii, the Head of IBM Quantum Japan and Senior Manager of Quantum-Centric Supercomputing SW.

The work of scalable quantum advantage is happening today at the University of Tokyo.