Published on October 22, 2025 8:27 PM GMT

I present a step-by-step argument in philosophy of mind. The main conclusion is that it is probably possible for conscious homomorphically encrypted digital minds to exist. This has surprising implications: it demonstrates a case where “mind exceeds physics” (epistemically), which implies the disjunction “mind exceeds reality” or “reality exceeds physics”. The main new parts of the discussion consist of (a) an argument that, if digital computers are conscious, so are homomorphically encrypted versions of them (steps 7-9); (b) speculation on the ontological consequences of homomorphically encrypted consciousness, in the form of a trilemma (steps 10-11).

Step 1. Physics

Let P be the set of possible physics states of the universe, according to “the true physics”. I am assuming that the intellectual project of physics has an idealized completion, which discovers a theory integrating all potentially accessible physical information. The theory will tend to be microscopic (although not necessarily strictly) and lawful (also not necessarily strictly). It need not integrate all real information, as some such information might not be accessible (e.g. in the case of the simulation hypothesis).

Rejecting this step: fundamental skepticism about even idealized forms of the intellectual project of physics; various religious/spiritual beliefs.

Step 2. Mind

Let M be the set of possible mental states of minds in the universe. Note, an element of M specifies something like a set or multiset of minds, as the universe could contain multiple minds. We don’t need M to be a complete theory of mind (specifying color qualia and so on); the main concern is doxastic facts, about beliefs of different agents. For example, I believe there is a wall behind me; this is a doxastic mental fact. This step makes no commitment to reductionism or non-reductionism. (Color qualia raise a number of semantic issues extraneous to this discussion; it is sufficient for now to consider mental states to be quotiented over any functionally equivalent color inversion/rotations, as these make no doxastic differences.)

Rejecting this step: eliminativism, especially eliminative physicalism.

Step 3. Reality

Let R be the set of possible reality states, according to “the true reality theory”. To motivate the idea, physics (P) only includes physical facts that could in principle be determined from the contents of our universe. There would remain basic ambiguities about the substrate, such as multiverse theories, or whether our universe exists in a computer simulation. R represents “the true theory of reality”, whatever that is; it is meant to include enough information to determine all that is real. For example, if physicalism is strictly true, then $R=P$, or is at least isomorphic. Solomonoff induction, and similarly the speed prior, posit that reality consists of an input to a universal Turing machine (specifying some other Turing machine and its input), and its execution trajectory, producing digital subjective experience.

Let $f:R\to P$ specify the universe’s physical state as a function of the reality state. Let $g:R\to M$ specify the universe’s mental state as a function of the reality state. These presumably exist under the above assumptions, because physics and mind are both aspects of reality, though these need not be efficiently computable functions. (The general structure of physics and mind being aspects of reality is inspired by neutral monism, though it does not necessitate neutral monism.)

Rejecting this step: fundamental doubt about the existence of a reality on which mind and physics supervene; incompatibilism between reality of mind and of physics.

Step 4. Natural supervenience

Similar to David Chalmers’s concept in The Conscious Mind. Informally, every possible physical state has a unique corresponding mental state. Formally:

$\forall (p:P),(\exists r:R,f(r)=p)\to (\exists !(m:M),\forall (r_2:R),(f\left(r_2\right)=p)\to g(r_2)=m)\left)\right)$

Here $\exists !$ means “there exists a unique”.

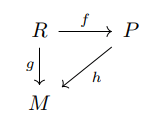
Assuming ZFC and natural supervenience, there exists the mapping function $h:P\to M$ commuting ($h\circ f=g$), though again, h need not be efficiently computable.

Natural supervenience is necessary for it to be meaningful to refer to the mental properties corresponding to some physical entity. For example, to ask about the mental state corresponding to a physical dog. Natural supervenience makes no strong claim about physics “causing” mind; it is rather a claim of constant conjunction, in the sense of Hume. We are not ruling out, for example, physics and mind being always consistent due to a common cause.

Rejecting this step: Interaction dualism. “Antenna theory”. Belief in P-zombies as not just logically possible, but really possible in this universe. Belief in influence of extra-physical entities, such as ghosts or deities, on consciousness.

Step 5. Digital consciousness

Assume it is possible for a digital computer running a program to be conscious. We don’t need to make strong assumptions about “abstract algorithms being conscious” here, just that realistic physical computers that run some program (such as a brain emulation) contain consciousness. This topic has been discussed to death, but to briefly say why I think digital computer consciousness is possible:

• The mind not being digitally simulable in a behaviorist manner (accepting normal levels of stochasticity/noise) would imply hypercomputation in physics, which is dubious.
• Chalmers’s fading qualia argument implies that, if a brain is gradually transformed into a behaviorally equivalent simulation, and the simulation is not conscious, then qualia must fade either gradually or suddenly; both are problematic.
• Having knowledge that no digital computer can be conscious would imply we have knowledge of ultimate reality $r:R$, specifically, that we do not exist in a digital computer simulation. While I don’t accept the simulation hypothesis as likely, it seems presumptuous to reject it on philosophy of mind grounds.

Rejecting this step: Brains as hypercomputers; or physical substrate dependence, e.g. only organic matter can be conscious.

Step 6. Real-physics fully homomorphic encryption is possible

Fully homomorphic encryption allows running a computation in an encrypted manner, producing an encrypted output; knowing the physical state of the computer and the output, without knowing the key, is insufficient to determine details of the computation or its output in physical polynomial time. Physical polynomial time is polynomial time with respect to the computing power of physics, BQP according to standard theories of quantum computation. Homomorphic encryption is not proven to work (since P != NP is not proven). However, quantum-resistant homomorphic encryption, e.g. based on lattices, is an active area of research, and is generally believed to be possible. This assumption says that (a) quantum-resistant homomorphic encryption is possible and (b) quantum-resistance is enough; physics doesn’t have more computing power than quantum. Or alternatively, non-quantum FHE is possible, and quantum computers are impossible. Or alternatively, the physical universe’s computation is more powerful than quantum, and yet FHE resisting it is still possible.

Rejecting this step: Belief that the physical universe has enough computing power to break any FHE scheme in polynomial time. Non-standard computational complexity theory (e.g. P = NP), cryptography, or physics.

Step 7. Homomorphically encrypted consciousness is possible

(Original thought experiment proposed by Scott Aaronson.)

Assume that a conscious digital computer can be homomorphically encrypted, and still be conscious, if the decryption key is available nearby. Since the key is nearby, the homomorphic encryption does not practically obscure anything. It functions more as a virtualization layer, similar to a virtual machine. If we already accept digital computer consciousness as possible, we need to tolerate some virtualization, so why not this kind?

An intuition backing this assumption is “can’t get something from nothing”. If we decrypt the output, we get the results that we would have gotten from running a conscious computation (perhaps including the entire brain emulation state trajectory in the output), so we by default assume consciousness happened in the process. We got the results without any fancy brain lesioning (to remove the seat of consciousness while preserving functional behavior), just a virtualization step.

As a concrete example, consider if someone using brain emulations as workers in a corporation decided to homomorphically encrypt the emulation (and later decrypt the results with a key on hand), to get the results of the work, without any subjective experience of work. It would seem dubious to claim that no consciousness happened in the course of the work (which could even include, for example, writing papers about consciousness), due to the homomorphic encryption layer.

As with digital consciousness, if we knew that homomorphically encrypted computations (with a nearby decryption key) were not conscious, then we would know something about ultimate reality, namely that we are not in a homomorphically encrypted simulation.

Rejecting this step: Picky quasi-functionalism. Enough multiple realizability to get digital computer consciousness, but not enough to get homomorphically encrypted consciousness, even if the decryption key is right there.

Step 8. Moving the key further away doesn’t change things

Now that the homomorphically encrypted conscious mind is separated from the key, consider moving the key 1 centimeter further away. We assume this doesn’t change the consciousness of the system, as long as the key is no more than 1 light-year away, so that it is in principle possible to retrieve the key. We can iterate to move the key 1 light-year away in small steps, without changing the consciousness of the overall system.

As an intuition, suppose the contrary that the computation with the nearby key was conscious, but not with the far-away key. We run the computation, still encrypted, to completion, while the key is far away. Then we bring the key back and decrypt it. It seems we “got something from nothing” here: we got the results of a conscious computation with no corresponding consciousness, and no fancy brain lesioning, just a virtualization layer with extra steps.

Rejecting this step: Either a discrete jump where moving the key 1 cm removes consciousness (yet consciousness can be brought back by moving the key back 1cm?), or a continuous gradation of diminished consciousness across distance, though somehow making no behavioral difference.

Step 9. Deleting a far-away key doesn’t change things

Suppose the system of the encrypted computation and the far-away key is conscious. Now suppose the key is destroyed. Assume this doesn’t affect the system’s consciousness: the encrypted computation by itself, with no key anywhere in the universe, is still conscious.

This assumption is based on locality intuition. Could my consciousness depend directly on events happening 1 light-year away, which I have no way of observing? If my consciousness depended on it in a behaviorally relevant way, then that would imply faster-than-light communication. So it can only depend on it in a behaviorally irrelevant way, but this presents similar problems as with P-zombies.

We could also consider a hypothetical where the key is destroyed, but then randomly guessed or brute-forced later. Does consciousness flicker off when the key is destroyed, then on again as it is guessed? Not in any behaviorally relevant way. We did something like “getting something from nothing” in this scenario, except that the key-guessing is real computational work. The idea that key-guessing is itself what is producing consciousness is highly dubious, due to the dis-analogy between the computation of key-guessing and the original conscious computation.

Rejecting this step: Consciousness as a non-local property, affected by far-away events, though not in a way that makes any physical difference. Global but not local natural supervenience.

Step 10. Physics does not efficiently determine encrypted mind

If a homomorphically encrypted mind (with no decryption key) is conscious, and has mental states such as belief, it seems it knows things (about its mental states, or perhaps mathematical facts) that cannot be efficiently determined from physics, using the computation of physics and polynomial time. Physical omniscience about the present state of the universe is insufficient to decrypt the computation. This is basically re-stating that homomorphic encryption works.

Imagine you learn you are in such an encrypted computation. It seems you know something that a physically omniscient agent doesn’t know except with super-polynomial amounts of computation: the basic contents of your experience, which could include the decryption key, or the solution to a hard NP complete problem.

There is a slight complication, in that perhaps the mental state can be determined from the entire trajectory of the universe, as the key was generated at some point in the past, even if every trace of it has been erased. However, in this case we are imagining something like Laplace’s demon looking at the whole physics history; this would imply that past states are “saved”, efficiently available to Laplace’s demon. (The possibility of real information, such as the demon’s memory of the physical trajectory, exceeding physical information, is discussed later; “Reality exceeds physics, informationally”.)

If locality of natural supervenience applies temporally, not just spatially, then the consciousness of the homomorphically encrypted computation can’t depend directly on the far past, only at most the recent past. In principle, the initial state of the homomorphically encrypted computation could have been “randomly initialized”, not generated from any existent original key, although of course this is unlikely.

So I assume that, given the steps up to here, the homomorphically encrypted mind really does know something (e.g. about its own experiences/beliefs, or mathematical facts) that goes beyond what can be efficiently inferred from physics, given the computing power of physics.

Rejecting this step: Temporal non-locality. Mental states depend on distinctions in the distant physical past, even though these distinctions make no physical or behavioral difference in the present or recent past. Doubt that the randomly initialized homomorphically encrypted mind really “knows anything” beyond what can be efficiently determined from physics, even reflexive properties about its own experience.

Step 11. A fork in the road

A terminological disambiguation: by P-efficiently computable, I mean computable in polynomial time with respect to the computing power of physics, which is BQP according to standard theories. By R-efficiently computable, I mean computable in polynomial time with respect to the computing power of reality, which is at least that of physics, but could in principle be higher, e.g. if our universe was simulated in a universe with beyond-quantum computation.

If assumptions so far are true, then there is no P-efficiently computable $h:P\to M$ mapping physical states to mental states, corresponding to the natural supervenience relation. This is because, in the case of homomorphically encrypted computation, h would have to run in P-super-polynomial time. This can be summarized as “mind exceeds physics, epistemically”: some mind in the system knows something that cannot be P-efficiently determined from physics, such as the solution to some hard NP-complete problem.

Now we ask a key question: Is there a R-efficiently computable $g:\mathrm{R</s}$