Natural language generation (NLG) is challenging because human language is complex and unpredictable. A naive approach of generating words randomly one by one would not be meaningful to humans. Modern decoder-only transformer models have proven effective for NLG tasks when trained on large amounts of text data. These models can be huge, but their structure is relatively simple. In this article, you will learn how to create a Llama or GPT model for next-token prediction.

Let’s get started.

Creating a Llama or GPT Model for Next-Token Prediction Photo by Roman Kraft. Some rights reserved.

Overview

This article is divided into three parts; they are:

• Understanding the Architecture of Llama or GPT Model
• Creating a Llama or GPT Model for Pretraining
• Variations in the Architecture

Understanding the Architecture of Llama or GPT Model

The architecture of a Llama or GPT model is simply a stack of transformer blocks. Each transformer block consists of a self-attention sub-layer and a feed-forward sub-layer, with normalization and residual connections applied around each sub-layer. That’s all the model has.

The architecture of GPT-2 and Llama models is shown in the figure below.

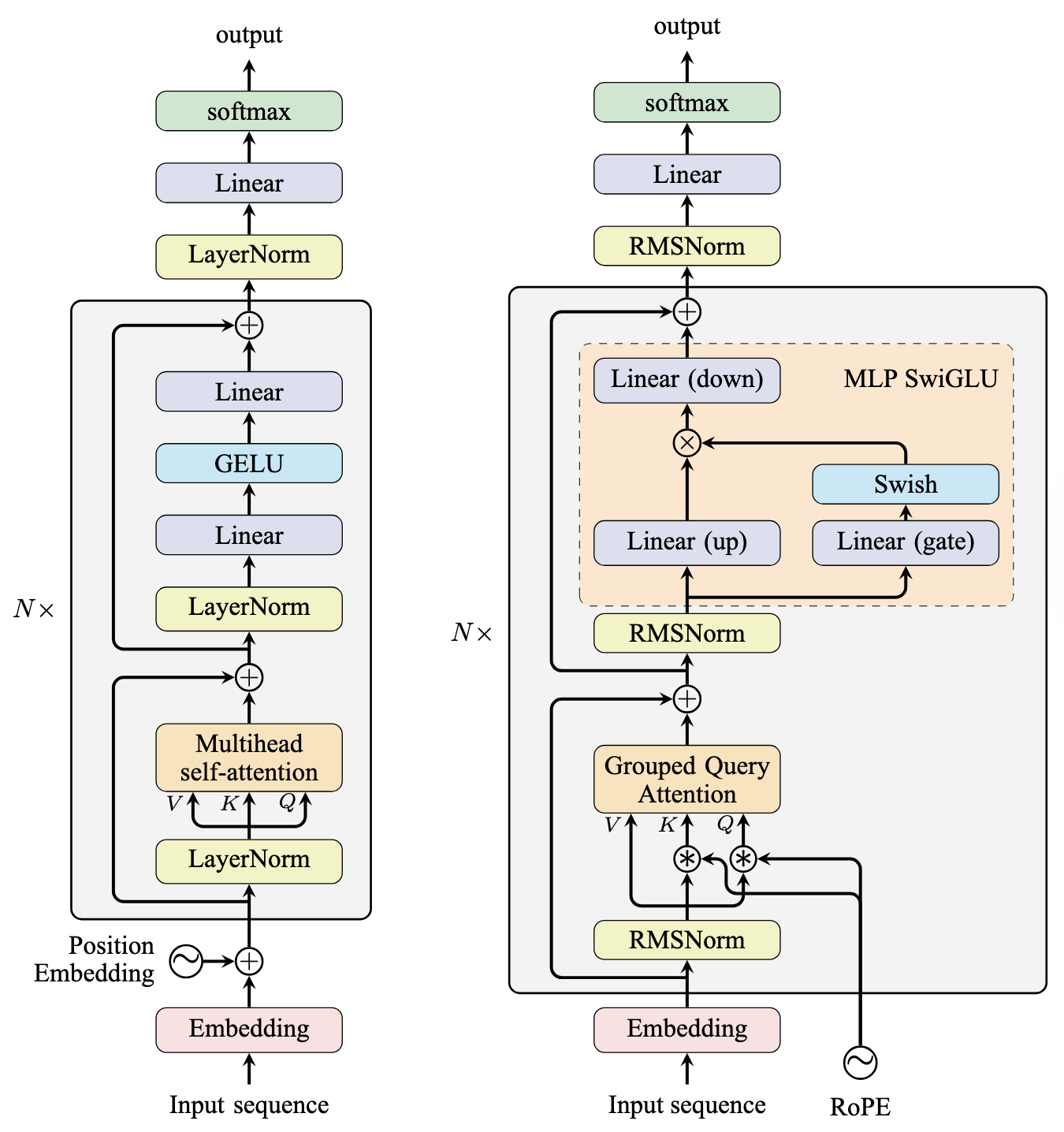
The GPT-2 (left) and Llama (right) model architectures

GPT-2 is older and mostly follows the architecture of the original encoder-decoder Transformer. It uses layer normalization and multi-headed attention, along with two linear layers in the feed-forward sub-layer. GPT-2 differs from the original transformer design in:

• Using pre-norm instead of post-norm
• Using learned position embeddings instead of sinusoidal embeddings
• Using GELU as the activation function in the feed-forward sub-layer instead of ReLU

Since GPT-2 is a decoder-only model, no encoder input is available, so the cross-attention sub-layer from the original transformer’s decoder stack is removed. However, you should not confuse its architecture with a transformer encoder because a causal mask is applied to the self-attention sub-layer, forcing the model to attend only to the left context.

The Llama model revised several aspects from GPT-2, and versions 1 through 3 of Llama share the same architecture. Like GPT-2, the Llama model is a decoder-only model that uses pre-norm. However, unlike GPT-2, the Llama model:

• Uses grouped query attention (GQA) instead of multi-headed attention (MHA)
• Uses rotary position embeddings (RoPE) instead of learned position embeddings or sinusoidal position embeddings, and this is applied at each self-attention sub-layer
• Uses SwiGLU as the activation function in the feed-forward sub-layer instead of ReLU, and because of that, the feed-forward sub-layer has three linear layers and an element-wise multiplication is involved
• Uses RMSNorm as the normalization function instead of LayerNorm

After the entire transformer stack, one more normalization layer is applied to the hidden state. The base model refers to the neural network from the input embedding through this final normalization layer.

For pretraining, you want the model to learn to predict the next token in a sequence. To do this, you add a pretraining head to the model—a linear layer that projects the hidden state to the vocabulary size. The softmax function is then used to get the probability distribution over the vocabulary.

Creating a Llama Model for Pretraining

There are many implementations of the Llama model available online. You can use existing code or create one using the Hugging Face transformers library if you care more about training results than understanding the model architecture. For example, the model created below is a Llama model with 12 layers and a pretraining head:

12345678	from transformers import LlamaForCausalLM, LlamaConfigconfig = LlamaConfig( num_hidden_layers=12, hidden_size=768, num_attention_heads=12)model = LlamaForCausalLM(config=config)

However, creating a Llama model from scratch using PyTorch is not difficult. First, let’s define a data class to hold the model configuration:

1234567891011

import dataclasses@dataclasses.dataclassclass LlamaConfig: vocab_size: int = 50000 # Size of the tokenizer vocabulary max_position_embeddings: int = 2048 # Maximum sequence length hidden_size: int = 768 # Dimension of hidden layers intermediate_size: int = 4*768 # Dimension of MLP’s hidden layer num_hidden_layers: int = 12 # Number of transformer layers num_attention_heads: int = 12 # Number of attention heads num_key_value_heads: int = 3 # Number of key-value heads for GQA

The model should have a fixed vocabulary size that matches the tokenizer you use. The maximum sequence length is a parameter for the rotary position embeddings and should be large enough to accommodate the longest sequence in your dataset. The hidden size, intermediate size, number of layers, and number of attention heads are hyperparameters that directly determine the model size and training or inference speed.

Rotary Position Embeddings

Let’s first implement the rotary position embeddings. Unlike other modules, the rotary position embeddings do not have any learnable parameters. Instead, they precompute the cosine and sine matrices and save them as buffers. Right before attention is computed, RoPE is applied to the query and key matrices. In formula, RoPE is applied as:

$$ \begin{aligned} Q_{s,i} &= Q_{s,i} \cos(s\theta_i) – Q_{s,\frac{d}{2}+i} \sin(s\theta_i) \ Q_{s,\frac{d}{2}+i} &= Q_{s,i} \sin(s\theta_i) + Q_{s,\frac{d}{2}+i} \cos(s\theta_i) \end{aligned} $$

where $Q_{s,i}$ is the $i$-th element of the token embedding of the query matrix $Q$ at sequence position $s$. The length of the token embedding (also known as the hidden size or the model dimension) is $d$. Applying RoPE to the key matrix $K$ is similar. The frequency term $\theta_i$ is computed as:

$$ \theta_i = \frac{1}{10000^{2i/d}} $$

To implement RoPE, you can use the following:

12345678910111213141516171819202122232425262728

import torch.nn as nndef rotate_half(x): """Rotates half the hidden dims of the input.""" x1, x2 = x.chunk(2, dim=-1) return torch.cat((-x2, x1), dim=-1)class RotaryPositionEncoding(nn.Module): def __init__(self, dim, max_position_embeddings): super().__init__() self.dim = dim self.max_position_embeddings = max_position_embeddings N = 10000.0 inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float() / dim)) inv_freq = torch.cat((inv_freq, inv_freq), dim=-1) position = torch.arange(max_position_embeddings).float() sinusoid_inp = torch.outer(position, inv_freq) self.register_buffer("cos", sinusoid_inp.cos()) self.register_buffer("sin", sinusoid_inp.sin()) def forward(self, x): """Apply RoPE to tensor x""" batch_size, seq_len, num_heads, head_dim = x.shape dtype = x.dtype cos = self.cos.to(dtype)[:seq_len].view(1, seq_len, 1, -1) sin = self.sin.to(dtype)[:seq_len].view(1, seq_len, 1, -1) output = (x * cos) + (rotate_half(x) * sin) return output

RoPE is a function to mutate the input tensor. To test the above RoPE module, you can do the following:

12345678	...import torchbatch_size, seq_len, hidden_size = 1, 10, 128max_position_embeddings = 2048x = torch.randn(batch_size, seq_len, hidden_size)rope = RotaryPositionEncoding(hidden_size, max_position_embeddings)x_rope = rope(x)

Self-Attention Sub-Layer

The self-attention sub-layer is the core of the transformer model. It is responsible for attending to the context of the input sequence. In Llama model, grouped query attention (GQA) is used, in which the key and value matrices are projected to fewer heads than the query matrix.

You do not need to implement GQA from scratch since PyTorch has a built-in implementation of GQA in the scaled_dot_product_attention function. You just need to pass the enable_gqa=True argument to the function.

Below is how you can implement the self-attention sub-layer:

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748

lass LlamaAttention(nn.Module): def __init__(self, config): super().__init__() self.hidden_size = config.hidden_size self.num_heads = config.num_attention_heads self.head_dim = self.hidden_size // self.num_heads self.num_kv_heads = config.num_key_value_heads # GQA: H_kv < H_q # hidden_size must be divisible by num_heads assert (self.head_dim * self.num_heads) == self.hidden_size # Linear layers for Q, K, V, and O projections self.q_proj = nn.Linear(self.hidden_size, self.num_heads * self.head_dim, bias=False) self.k_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.v_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.o_proj = nn.Linear(self.num_heads * self.head_dim, self.hidden_size, bias=False) def forward(self, hidden_states, rope, attn_mask): bs, seq_len, dim = hidden_states.size() # Project inputs to Q, K, V query_states = self.q_proj(hidden_states).view(bs, seq_len, self.num_heads, self.head_dim) key_states = self.k_proj(hidden_states).view(bs, seq_len, self.num_kv_heads, self.head_dim) value_states = self.v_proj(hidden_states).view(bs, seq_len, self.num_kv_heads, self.head_dim) # Apply rotary position embeddings query_states = rope(query_states) key_states = rope(key_states) # Transpose tensors from BSHD to BHSD dimension for scaled_dot_product_attention query_states = query_states.transpose(1, 2) key_states = key_states.transpose(1, 2) value_states = value_states.transpose(1, 2) # Use PyTorch’s optimized attention implementation attn_output = F.scaled_dot_product_attention( query_states, key_states, value_states, attn_mask=attn_mask, dropout_p=0.0, enable_gqa=True, ) # Transpose output tensor from BHSD to BSHD dimension, reshape to 3D, and then project output attn_output = attn_output.transpose(1, 2).reshape(bs, seq_len, self.hidden_size) attn_output = self.o_proj(attn_output) return attn_output

This is a few lines of code but not trivial. The attention block implements GQA self-attention with RoPE.

Upon entry, you project the input tensor to query, key, and value tensors using linear layers. Then you split the last dimension (corresponding to the token embeddings) into two parts: one for the number of heads and one for the dimension per head. Note that the original tensor has shape (batch_size, sequence_length, hidden_size), and after projection and reshaping, it has shape (batch_size, sequence_length, num_heads, head_dim). You should transpose this to (batch_size, num_heads, sequence_length, head_dim) before applying attention.

Computing GQA is straightforward. You simply call the scaled_dot_product_attention function with enable_gqa=True and pass the query, key, and value tensors. Note that the query tensor has more heads than the key and value tensors, but the number of query heads must be a multiple of the number of key and value heads.

For the output, you restore the tensor to its original shape and project it once more using a linear layer.

SwiGLU Sub-Layer

The feed-forward sub-layer in Llama model uses SwiGLU as the activation function. Mathematically, SwiGLU is defined as:

$$ \begin{aligned} \text{SwiGLU}(x) &= \text{swish}(xW_1 + b_1) \otimes (xW_2 + b_2) \ \text{swish}(x) &= \frac{x}{1 + e^{-x}} \end{aligned} $$

The symbol $\otimes$ represents element-wise multiplication of the two tensors. Effectively, the SwiGLU function models a quadratic function.

In GPT and Llama models, you expand the input tensor dimension to a larger size, apply the activation function, then project it back to the original dimension. This dimensional expansion is believed to enable learning more complex relationships between input and output.

PyTorch does not have a single function to implement SwiGLU. But you can implement it using the F.silu function and the element-wise multiplication, as follows:

1234567891011121314

class LlamaMLP(nn.Module): def __init__(self, config): super().__init__() # Two parallel projections for SwiGLU self.gate_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.up_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.act_fn = F.silu # SwiGLU activation function # Project back to hidden size self.down_proj = nn.Linear(config.intermediate_size, config.hidden_size, bias=False) def forward(self, x): gate = self.act_fn(self.gate_proj(x)) up = self.up_proj(x) return self.down_proj(gate * up)

Transformer Block

A GPT or Llama model is a stack of transformer blocks. To implement a transformer block, you simply process the input tensor through the self-attention sub-layer and the feed-forward sub-layer. The implementation is as follows:

1234567891011121314151617181920

class LlamaDecoderLayer(nn.Module): def __init__(self, config): super().__init__() self.input_layernorm = nn.RMSNorm(config.hidden_size, eps=1e-5) self.self_attn = LlamaAttention(config) self.post_attention_layernorm = nn.RMSNorm(config.hidden_size, eps=1e-5) self.mlp = LlamaMLP(config) def forward(self, hidden_states, rope, attn_mask): # First residual block: Self-attention residual = hidden_states hidden_states = self.input_layernorm(hidden_states) attn_outputs = self.self_attn(hidden_states, rope, attn_mask) hidden_states = attn_outputs + residual # Second residual block: MLP residual = hidden_states hidden_states = self.post_attention_layernorm(hidden_states) hidden_states = self.mlp(hidden_states) + residual return hidden_states

The attention and feed-forward sub-layers are the main components of the transformer block. You apply normalization before each sub-layer and add the residual connection afterward.

The forward() method accepts an input tensor, a RoPE module, and an attention mask tensor. The RoPE and attention mask are shared by all transformer blocks and should be created once, outside the blocks.

The Base Llama Model and the Pretraining Head

The base Llama model ties all the transformer blocks together. It creates the rotary position embeddings module to share across all transformer blocks.

With all the building blocks in place, the base Llama model is straightforward to implement:

1234567891011121314151617181920212223

class LlamaModel(nn.Module): def __init__(self, config): super().__init__() self.rotary_emb = RotaryPositionEncoding( config.hidden_size // config.num_attention_heads, config.max_position_embeddings, ) self.embed_tokens = nn.Embedding(config.vocab_size, config.hidden_size) self.layers = nn.ModuleList([ LlamaDecoderLayer(config) for _ in range(config.num_hidden_layers) ]) self.norm = nn.RMSNorm(config.hidden_size, eps=1e-5) def forward(self, input_ids, attn_mask): # Convert input token IDs to embeddings hidden_states = self.embed_tokens(input_ids) # Process through all transformer layers, then the final norm layer for layer in self.layers: hidden_states = layer(hidden_states, rope=self.rotary_emb, attn_mask=attn_mask) hidden_states = self.norm(hidden_states) # Return the final hidden states return hidden_states

The base model expects an integer tensor of token IDs as input. This is transformed into a floating-point tensor of embedding vectors using the embedding layer. These are the “hidden states” that are transformed through each block. The output from the last block is normalized once more as the final output of the model.

Note that a rotary position embeddings module is created in the constructor and passed to each transformer block in the forward() method. This allows efficient sharing of RoPE calculations across all blocks.

As a final step, you would need a pretraining model, as follows:

123456789	class LlamaForPretraining(nn.Module): def __init__(self, config): super().__init__() self.base_model = LlamaModel(config) self.lm_head = nn.Linear(config.hidden_size, config.vocab_size, bias=False) def forward(self, input_ids, attn_mask): hidden_states = self.base_model(input_ids, attn_mask) return self.lm_head(hidden_states)

This is simply one additional linear layer applied to the output of the base model. This linear layer is large because it projects the hidden state to the vocabulary size. The output of this layer is the logits for the next token in the vocabulary. You should not include a softmax layer in the model for two reasons:

1. In PyTorch, the cross-entropy loss function expects the logits, not the probabilities. 2. During inference, you may want to compute the softmax probabilities with a custom temperature. It is better to leave it outside the model to retain the flexibility.

That’s all you need to create a Llama model for pretraining!

Attention Masks

From the code above, you can see that the Llama model expects an integer tensor of token IDs and an attention mask tensor as input. The token ID tensor has shape (batch_size, sequence_length), and the attention mask tensor has shape (batch_size, 1, sequence_length, sequence_length). This is because the attention function produces attention weights of shape (batch_size, num_heads, sequence_length, sequence_length), and the mask must be broadcastable to this shape.

You could modify the model to accept only the token ID tensor and generate a causal attention mask automatically. However, for training, it’s better to control the attention mask explicitly so you can mask out padding tokens or other unwanted tokens in the batch.

Generating a mask that handles both causal masking and padding is straightforward. Below is code to generate a random input tensor with some padding tokens and then create the corresponding causal and padding masks:

1234567891011121314151617181920212223242526

def create_causal_mask(seq_len, device, dtype): mask = torch.full((seq_len, seq_len), float(‘-inf’), device=device, dtype=dtype) \ .triu(diagonal=1) return maskdef create_padding_mask(batch, padding_token_id, device, dtype): padded = torch.zeros_like(batch, device=device, dtype=dtype) \ .masked_fill(batch == padding_token_id, float(‘-inf’)) mask = padded[:,:,None] + padded[:,None,:] return mask[:, None, :, :]# create a random input tensorPAD_TOKEN_ID = 0device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")bs, seq_len = 5, 13x = torch.randint(1, test_config.vocab_size, (bs, seq_len), dtype=torch.int32, device=device)# set padding tokens at the end of each sequencefor i, pad_length in enumerate([4, 1, 0, 3, 8]): if pad_length > 0: x[i, -pad_length:] = PAD_TOKEN_ID# Create causal and padding maskscausal_mask = create_causal_mask(seq_len, device)padding_mask = create_padding_mask(x, PAD_TOKEN_ID, device)attn_mask = causal_mask + padding_maskprint(f"Input ids: {x}")print(f"Attention mask: {attn_mask}")

A sequence of length $N$ (excluding padding tokens) should have a triangular mask matrix of shape $N\times N$ with all above-diagonal elements (and all elements outside this $N\times N$ range) set to $-\infty$.

To test the model you built, you can run it with a random input to ensure no errors are raised:

12345678910	...test_config = LlamaConfig()device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")model = LlamaModel(test_config).to(device)# print the model sizeprint(f"Model parameters size: {sum(p.numel() for p in model.parameters()) / 1024**2:.2f} M")print(f"Model buffers size: {sum(p.numel() for p in model.buffers()) / 1024**2:.2f} M")output = model(x, attn_mask)print("OK")

You should see this model is really small, only 134.51M parameters. But it is good enough as a toy project to learn how to implement a language model from scratch.

Below is the complete code:

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268

import dataclassesimport torchimport torch.nn as nnimport torch.nn.functional as Ffrom torch import Tensor@dataclasses.dataclassclass LlamaConfig: """Define Llama model hyperparameters.""" vocab_size: int = 50000 # Size of the tokenizer vocabulary max_position_embeddings: int = 2048 # Maximum sequence length hidden_size: int = 768 # Dimension of hidden layers intermediate_size: int = 4*768 # Dimension of MLP’s hidden layer num_hidden_layers: int = 12 # Number of transformer layers num_attention_heads: int = 12 # Number of attention heads num_key_value_heads: int = 3 # Number of key-value heads for GQAdef rotate_half(x: Tensor) -> Tensor: """Rotates half the hidden dims of the input. This is a helper function for rotary position embeddings (RoPE). For a tensor of shape (..., d), it returns a tensor where the last d/2 dimensions are rotated by swapping and negating. Args: x: Input tensor of shape (..., d) Returns: Tensor of same shape with rotated last dimension """ x1, x2 = x.chunk(2, dim=-1) return torch.cat((-x2, x1), dim=-1) # Concatenate with rotationclass RotaryPositionEncoding(nn.Module): """Rotary position encoding.""" def __init__(self, dim: int, max_position_embeddings: int) -> None: """Initialize the RotaryPositionEncoding module Args: dim: The hidden dimension of the input tensor to which RoPE is applied max_position_embeddings: The maximum sequence length of the input tensor """ super().__init__() self.dim = dim self.max_position_embeddings = max_position_embeddings # compute a matrix of n\theta_i N = 10_000.0 inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float() / dim)) inv_freq = torch.cat((inv_freq, inv_freq), dim=-1) position = torch.arange(max_position_embeddings).float() sinusoid_inp = torch.outer(position, inv_freq) # save cosine and sine matrices as buffers, not parameters self.register_buffer("cos", sinusoid_inp.cos()) self.register_buffer("sin", sinusoid_inp.sin()) def forward(self, x: Tensor) -> Tensor: """Apply RoPE to tensor x Args: x: Input tensor of shape (batch_size, seq_length, num_heads, head_dim) Returns: Output tensor of shape (batch_size, seq_length, num_heads, head_dim) """ batch_size, seq_len, num_heads, head_dim = x.shape dtype = x.dtype # transform the cosine and sine matrices to 4D tensor and the same dtype as x cos = self.cos.to(dtype)[:seq_len].view(1, seq_len, 1, -1) sin = self.sin.to(dtype)[:seq_len].view(1, seq_len, 1, -1) # apply RoPE to x output = (x * cos) + (rotate_half(x) * sin) return outputclass LlamaAttention(nn.Module): """Grouped-query attention with rotary embeddings.""" def __init__(self, config: LlamaConfig) -> None: super().__init__() self.hidden_size = config.hidden_size self.num_heads = config.num_attention_heads self.head_dim = self.hidden_size // self.num_heads self.num_kv_heads = config.num_key_value_heads # GQA: H_kv < H_q # hidden_size must be divisible by num_heads assert (self.head_dim * self.num_heads) == self.hidden_size # Linear layers for Q, K, V projections self.q_proj = nn.Linear(self.hidden_size, self.num_heads * self.head_dim, bias=False) self.k_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.v_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.o_proj = nn.Linear(self.num_heads * self.head_dim, self.hidden_size, bias=False) def forward(self, hidden_states: Tensor, rope: RotaryPositionEncoding, attn_mask: Tensor) -> Tensor: bs, seq_len, dim = hidden_states.size() # Project inputs to Q, K, V query_states = self.q_proj(hidden_states).view(bs, seq_len, self.num_heads, self.head_dim) key_states = self.k_proj(hidden_states).view(bs, seq_len, self.num_kv_heads, self.head_dim) value_states = self.v_proj(hidden_states).view(bs, seq_len, self.num_kv_heads, self.head_dim) # Apply rotary position embeddings query_states = rope(query_states) key_states = rope(key_states) # Transpose tensors from BSHD to BHSD dimension for scaled_dot_product_attention query_states = query_states.transpose(1, 2) key_states = key_states.transpose(1, 2) value_states = value_states.transpose(1, 2) # Use PyTorch’s optimized attention implementation # setting is_causal=True is incompatible with setting explicit attention mask attn_output = F.scaled_dot_product_attention( query_states, key_states, value_states, attn_mask=attn_mask, dropout_p=0.0, enable_gqa=True, ) # Transpose output tensor from BHSD to BSHD dimension, reshape to 3D, and then project output attn_output = attn_output.transpose(1, 2).reshape(bs, seq_len, self.hidden_size) attn_output = self.o_proj(attn_output) return attn_outputclass LlamaMLP(nn.Module): """Feed-forward network with SwiGLU activation.""" def __init__(self, config: LlamaConfig) -> None: super().__init__() # Two parallel projections for SwiGLU self.gate_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.up_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.act_fn = F.silu # SwiGLU activation function # Project back to hidden size self.down_proj = nn.Linear(config.intermediate_size, config.hidden_size, bias=False) def forward(self, x: Tensor) -> Tensor: # SwiGLU activation: multiply gate and up-projected inputs gate = self.act_fn(self.gate_proj(x)) up = self.up_proj(x) return self.down_proj(gate * up)class LlamaDecoderLayer(nn.Module): """Single transformer layer for a Llama model.""" def __init__(self, config: LlamaConfig) -> None: super().__init__() self.input_layernorm = nn.RMSNorm(config.hidden_size, eps=1e-5) self.self_attn = LlamaAttention(config) self.post_attention_layernorm = nn.RMSNorm(config.hidden_size, eps=1e-5) self.mlp = LlamaMLP(config) def forward(self, hidden_states: Tensor, rope: RotaryPositionEncoding, attn_mask: Tensor) -> Tensor: # First residual block: Self-attention residual = hidden_states hidden_states = self.input_layernorm(hidden_states) attn_outputs = self.self_attn(hidden_states, rope=rope, attn_mask=attn_mask) hidden_states = attn_outputs + residual # Second residual block: MLP residual = hidden_states hidden_states = self.post_attention_layernorm(hidden_states) hidden_states = self.mlp(hidden_states) + residual return hidden_statesclass LlamaModel(nn.Module): """The full Llama model without any pretraining heads.""" def __init__(self, config: LlamaConfig) -> None: super().__init__() self.rotary_emb = RotaryPositionEncoding( config.hidden_size // config.num_attention_heads, config.max_position_embeddings, ) self.embed_tokens = nn.Embedding(config.vocab_size, config.hidden_size) self.layers = nn.ModuleList([LlamaDecoderLayer(config) for _ in range(config.num_hidden_layers)]) self.norm = nn.RMSNorm(config.hidden_size, eps=1e-5) def forward(self, input_ids: Tensor, attn_mask: Tensor) -> Tensor: # Convert input token IDs to embeddings hidden_states = self.embed_tokens(input_ids) # Process through all transformer layers, then the final norm layer for layer in self.layers: hidden_states = layer(hidden_states, rope=self.rotary_emb, attn_mask=attn_mask) hidden_states = self.norm(hidden_states) # Return the final hidden states return hidden_statesclass LlamaForPretraining(nn.Module): def __init__(self, config: LlamaConfig) -> None: super().__init__() self.base_model = LlamaModel(config) self.lm_head = nn.Linear(config.hidden_size, config.vocab_size, bias=False) def forward(self, input_ids: Tensor, attn_mask: Tensor) -> Tensor: hidden_states = self.base_model(input_ids, attn_mask) return self.lm_head(hidden_states)def create_causal_mask(seq_len: int, device: torch.device, dtype: torch.dtype = torch.float32) -> Tensor: """Create a causal mask for self-attention. Args: seq_len: Length of the sequence device: Device to create the mask on dtype: Data type of the mask Returns: Causal mask of shape (seq_len, seq_len) """ mask = torch.full((seq_len, seq_len), float(‘-inf’), device=device, dtype=dtype) \ .triu(diagonal=1) return maskdef create_padding_mask(batch, padding_token_id, device: torch.device, dtype: torch.dtype = torch.float32): """Create a padding mask for a batch of sequences for self-attention. Args: batch: Batch of sequences, shape (batch_size, seq_len) padding_token_id: ID of the padding token Returns: Padding mask of shape (batch_size, 1, seq_len, seq_len) """ padded = torch.zeros_like(batch, device=device, dtype=dtype) \ .masked_fill(batch == padding_token_id, float(‘-inf’)) mask = padded[:,:,None] + padded[:,None,:] return mask[:, None, :, :]# Create model with default configtest_config = LlamaConfig()device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")model = LlamaModel(test_config).to(device)# print the model sizeprint(f"Model parameters size: {sum(p.numel() for p in model.parameters()) / 1024**2:.2f} MB")print(f"Model buffers size: {sum(p.numel() for p in model.buffers()) / 1024**2:.2f} MB")# Create a random tensorPAD_TOKEN_ID = 0bs, seq_len = 5, 13x = torch.randint(1, test_config.vocab_size, (bs, seq_len), dtype=torch.int32, device=device)# set random length of padding tokens at the end of each sequencefor i, pad_length in enumerate([4, 1, 0, 3, 8]): if pad_length > 0: x[i, -pad_length:] = PAD_TOKEN_ID# Create causal and padding maskscausal_mask = create_causal_mask(seq_len, device)padding_mask = create_padding_mask(x, PAD_TOKEN_ID, device)attn_mask = causal_mask + padding_maskprint(f"Input ids: {x}")print(f"Attention mask: {attn_mask}")# Run the modeloutput = model(x, attn_mask)print("OK")

Variations in the Architecture

The code above implements the base Llama model. It is straightforward to change the implementation to a GPT model by removing RoPE and replacing it with a learned position embeddings layer in the base model, replacing RMSNorm with LayerNorm, turning off GQA, and using a GELU feed-forward sub-layer instead of SwiGLU.

If you want to design your own decoder-only transformer model, you are not required to follow the exact architecture of Llama or GPT. Besides basic hyperparameters such as vocabulary size or number of transformer layers, here are some variations you may consider:

• In the implementation above, the nn.Linear layers deliberately use bias=False to skip the bias term. This trims the model size slightly and makes the model faster to train. You may want to add the bias term to make the model more flexible in learning complex patterns.
• The feed-forward sub-layer effectively consists of an upward projection, a SwiGLU activation, and a downward projection. This is the “two-layer MLP” pattern. You could explore a three-layer MLP by adding one more projection and activation function. Three-layer MLPs are known to learn more complex patterns than two-layer MLPs.
• Newer generations of transformer models (such as Llama 4) use Mixture of Experts (MoE) to replace the feed-forward sub-layer. This is known to be more efficient to train than simply making the feed-forward sub-layer larger and is useful for larger models that need to learn more complex patterns.

Further Readings

Below are some resources that you may find useful:

• Radford et al. (2019) Language Models are Unsupervised Multitask Learners (the GPT-2 paper)
• Brown et al. (2020) Language Models are Few-Shot Learners (the GPT-3 paper)
• Touvron et al. (2023) Llama: Open and Efficient Foundation Language Models (the Llama paper)
• Grattafiori et al. (2024) The Llama 3 Herd of Models (the Llama 3 paper)
• Gerber (2025) Attention Is Not All You Need: The Importance of Feedforward Networks in Transformer Models

Summary

In this article, you learned how to create a Llama model for next-token prediction from scratch using PyTorch. Specifically, you learned:

• The building blocks of a decoder-only transformer model
• The architectural differences between Llama and GPT
• How to implement all the building blocks of a Llama model
• What are the variations in the architecture that you may explore

No comments yet.

Leave a Reply